今回も「気温以外のデータ」を使って,さらに線形二項分類の時よりも観測データを多くして,太平洋側の都市と日本海側の都市を比較してみる.
因子分析
因子分析とは,観測された変数の「原因となっている何らかの変数」が隠れて存在する(潜在変数)と考え,その変数を探す分析のことである.
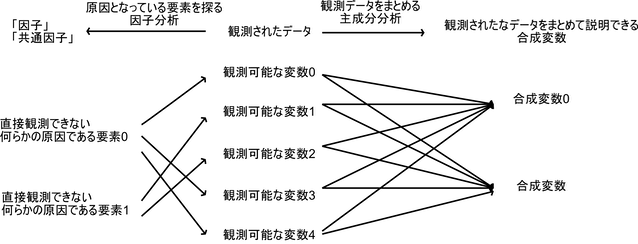
例えば太平洋側の都市と日本海側の都市では冬の気候に大きな違いがあるが,観測データには何らかの「観測可能なデータの違い」があり,その観測可能なデータから「原因」である「気候の違い」を,「なるべく少ない要素」で表現できるように探すことが目的である.
「どちらか側の海」というのは根本的な原因であるダミー変数だが,ダミー変数を直接出せるほど因子分析は優れてはいないので,潜在変数はスカラ値であることがほとんどである.
次元圧縮としても使えてしまうため,主成分分析と混同されることがあるが,因子分析と主成分分析は考え方が逆である.
因子分析は「観測可能なデータから,観測データの原因となっている少数の要素(因子,潜在変数)があると仮定して,それを推測する」
主成分分析は「観測可能なデータから,少数で多くの観測データを上手く表現することができる少数の合成変数を作成する」
である.
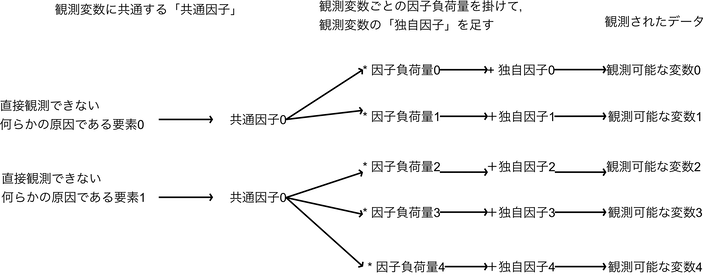
実際には「共通因子」に,どのぐらい共通因子が占める割合が大きいかの「因子負荷量」を掛け,その変数の独自の要素である「独自因子」を足したものが,観測データである.
因子分析の特徴として,因子の数がいくつあるかを与えなければならない.因子分析の手法は多く提唱されており色々な組み合わせがあるが,「回転法」が直交法 - Varimax回転の時に因子数の指標となるのが「因子負荷量」である.
因子負荷量は,その仮定した因子がどのぐらい各観測変数に影響を与えているか(正確には各観測変数と各因子の相関係数,つまり連動して動いているか)を見るもので,因子負荷量が各変数において各因子間の違いが大きければ大きいほど,その仮定した因子数は適切である,と考える.(相関係数なので-1から1の間に収まる.0の時は「観測変数とその因子は全く連動していない」ということになる.)
具体的には,「各変数の各因子に対する因子負荷量を見て,一つの因子のみ1(もしくは-1)に近く,他の因子は0に近い」場合には,その因子の選定は適切である,となる.
データの取得と加工
例によって,気象庁オープンデータのページから,
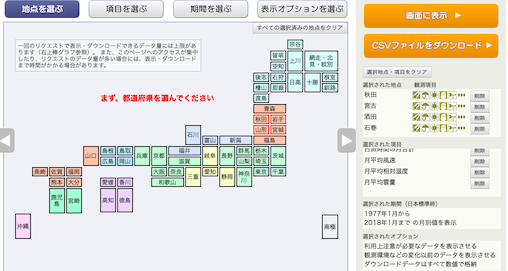
都市は,秋田県→秋田市,岩手県→宮古市,山形県→酒田市,宮城県→石巻市,の順で,それぞれ選択.
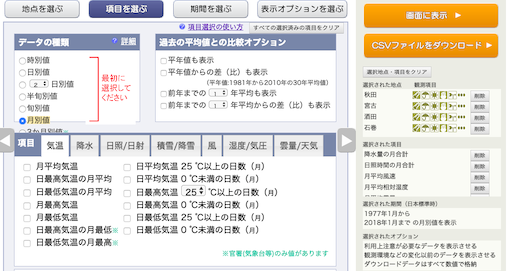
今回も「気温以外のデータ」なので,気温は選択しない.
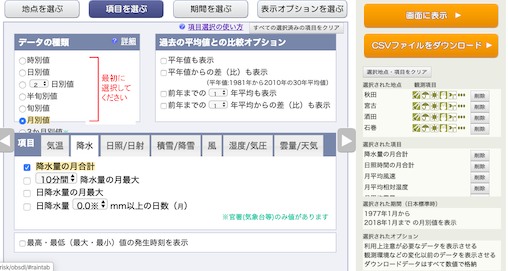
月別の値を選択し,降水量の月合計,
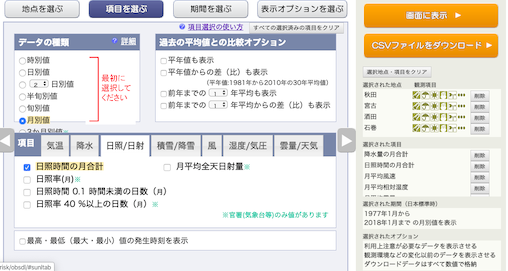
日照時間の月合計,
月平均風速,
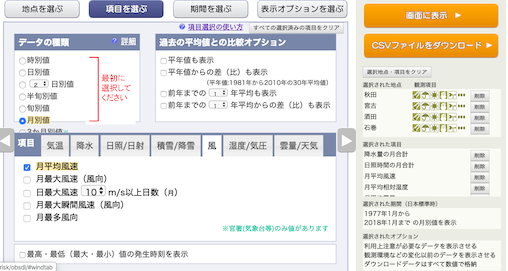
湿度/気圧の月平均蒸気圧,を選択し,
平均雲量,を選択し,
1977年〜2018年の「1月」のデータをダウンロードする.
表示オプションはデフォルト.地点の順番と,項目の順番を確認すること.
Googleスプレッドシートに読み込む.スタック形式のデータにする.
いつものように不要な行と列を削除.年月の列も使わないので削除.
一番左の列を選択肢,右クリック→「1列左に挿入」で,「観測地点」を記入する列を挿入
作られた列の冒頭に「観測地点」の列名を記入.
観測地点列に「秋田」を入力.
宮古の観測データを洗濯して,右クリック→「切り取り」
秋田の下に貼り付ける.一番左は「観測地点」列なので,列を間違わないこと.
観測地点列に「宮古」を入力.
同じく酒田のデータを作成.
同じく石巻のデータを作成.
列名を短く整える.
これまでと同じ様に,ファイル→ウェブに公開.
CSV形式でウェブに公開してURLをコピーしておく.
いつものようにRに読み込んで,最初の数行を表示する.
url <- '公開したURL'
df <- read.csv(url, header=TRUE)
head(df)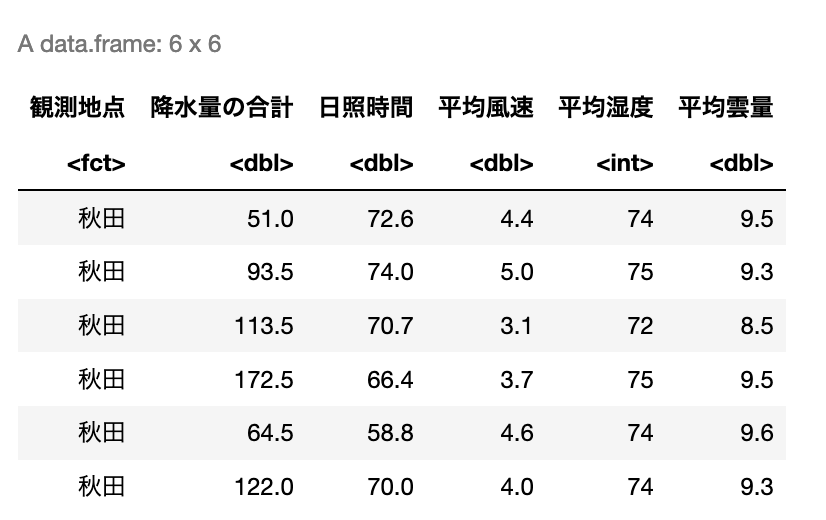
欠損データ行の削除
データ加工の途中でわかったと思うが「平均雲量」は欠損が大きい.(おそらく気象庁内で観測基準が変わったため?)欠損している行を削除する必要がある.
t検定の項でもやったが,欠損地がある行を丸ごと削除するのは以下のプログラムである.
# 欠損値のある行を削除して,df変数に再代入
df <- na.omit(df)psychパッケージの中の因子分析関数fa
Rの標準の因子分析パッケージは,共通因子が2で固定など,ほぼ役に立たないので,psychパッケージの中に入っているfa間数を使う.
# ライブラリを使う宣言
library("psych")
library("GPArotation") # こっちは回転に使うライブラリ共通因子数の決定
因子分析は,最初に「幾つの共通因子があるか」を与えなければならない.共通因子数を変えながら探索的に共通因子数を探ることを「探索的因子分析」と呼ぶのだが,psychパッケージの中には,この共通因子数を提案してくれるfa.parallelという関数が存在する.
# 因子分析に食わせるのは,観測値なので,観測地点はいらない
df.X <- df[, c('降水量の合計', '日照時間', '平均風速', '平均湿度', '平均雲量')]
fa.parallel(df.X)結果は以下のようになる.
Parallel analysis suggests that the number of factors = 1 and the number of components = 1 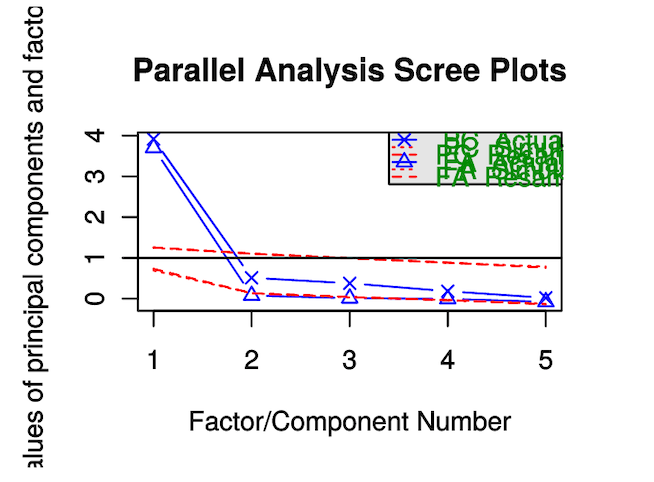
共通因子数1で説明できると提案されてしまった.
つまり,何か1つの共通する要素だけで,観測値が説明できるんでは?ということになる.
1だと2次元散布図に描きづらいので,共通因子数1の場合と2の場合で実行してみよう.<
psychパッケージのfa関数による因子分析の実行 varimax回転
まず共通因子数1の場合,
result.fa <-fa(r=df.X, nfactors=1, fm="ml", rotate="varimax")
print(result.fa, digits=3, sort=TRUE) #digitsオプションは小数点以下の桁数,sortオプションは表示順が並べ替えられる.
r=オプションはデータを与える.nfactors=共通因子数オプションで,共通因子数を与える.fm=オプションは算出法であり,とりあえず今回は一般的な最尤法であるmlを指定しておく.rotation=オプションは回転方法を与える.varimax法を与えておく.
結果は以下のようになる.
Factor Analysis using method = ml
Call: fa(r = df.X, nfactors = 1, rotate = "varimax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
V ML1 h2 u2 com
平均雲量 5 0.998 0.995 0.00498 1
日照時間 2 -0.976 0.953 0.04741 1
平均風速 3 0.853 0.727 0.27305 1
降水量の合計 1 0.717 0.515 0.48520 1
平均湿度 4 0.713 0.508 0.49165 1
ML1
SS loadings 3.698
Proportion Var 0.740
Mean item complexity = 1
Test of the hypothesis that 1 factor is sufficient.
The degrees of freedom for the null model are 10 and the objective function was 5.972 with Chi Square of 773.424
The degrees of freedom for the model are 5 and the objective function was 0.306
The root mean square of the residuals (RMSR) is 0.026
The df corrected root mean square of the residuals is 0.037
The harmonic number of observations is 133 with the empirical chi square 1.849 with prob < 0.87
The total number of observations was 133 with Likelihood Chi Square = 39.442 with prob < 1.93e-07
Tucker Lewis Index of factoring reliability = 0.9093
RMSEA index = 0.2316 and the 90 % confidence intervals are 0.1654 0.2972
BIC = 14.99
Fit based upon off diagonal values = 0.999
Measures of factor score adequacy
ML1
Correlation of (regression) scores with factors 0.998
Multiple R square of scores with factors 0.996
Minimum correlation of possible factor scores 0.991同じように共通因子数2の因子分析を実行する.
result.fa <- fa(r=df.X, nfactors=2, fm="ml", rotate="varimax")
print(result.fa, digits=3, sort=TRUE)結果は以下のようになる.
Factor Analysis using method = ml
Call: fa(r = df.X, nfactors = 2, rotate = "varimax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
item ML1 ML2 h2 u2 com
日照時間 2 -0.927 -0.368 0.995 0.00497 1.31
平均雲量 5 0.848 0.509 0.978 0.02187 1.64
平均風速 3 0.711 0.485 0.740 0.26015 1.76
降水量の合計 1 0.679 0.286 0.543 0.45739 1.34
平均湿度 4 0.364 0.803 0.778 0.22222 1.39
ML1 ML2
SS loadings 2.677 1.356
Proportion Var 0.535 0.271
Cumulative Var 0.535 0.807
Proportion Explained 0.664 0.336
Cumulative Proportion 0.664 1.000
Mean item complexity = 1.5
Test of the hypothesis that 2 factors are sufficient.
The degrees of freedom for the null model are 10 and the objective function was 5.972 with Chi Square of 773.424
The degrees of freedom for the model are 1 and the objective function was 0.02
The root mean square of the residuals (RMSR) is 0.011
The df corrected root mean square of the residuals is 0.033
The harmonic number of observations is 133 with the empirical chi square 0.293 with prob < 0.588
The total number of observations was 133 with Likelihood Chi Square = 2.549 with prob < 0.11
Tucker Lewis Index of factoring reliability = 0.9795
RMSEA index = 0.111 and the 90 % confidence intervals are 0 0.2821
BIC = -2.341
Fit based upon off diagonal values = 1
Measures of factor score adequacy
ML1 ML2
Correlation of (regression) scores with factors 0.975 0.877
Multiple R square of scores with factors 0.951 0.768
Minimum correlation of possible factor scores 0.903 0.537因子負荷量
それぞれの結果の最初の表のML1が1番目の共通因子の「因子負荷量」(以下ML2も同じ),h2列が「共通性」,u2は「独自性」.
前述の因子分析が想定するモデルで「「共通因子」に「独自因子」を足したものが観測変数として現れている」という説明を図でしたが,この「共通因子」に依存している割合が「共通性」であり,その逆「1-共通性」が「独自性」である.
重量なのが,各共通因子と各観測変数の間の「因子負荷量」である.因子負荷量は「その因子が変数つまり観測された値にどれだけ影響を与えているか」の値で,-1から1の間を取る.
因子分析が「うまくいった」と判断される因子負荷量は「1観測変数に対して,1共通因子だけ1もしくは-1に近く,他の共通因子では0に近い」である.逆に.1つの観測変数に対して因子負荷量の共通因子間の差が小さい場合は因子分析がうまくいかなかったことを示している.
共通因子数2を与えた例では,日照時間に関して,負の方向では因子間の違いがあまりない(共通因子2と4の間がほとんど差がない)ことから,因子分析がうまくいっておらず,共通因子数4を仮定するのは,あまり具合が良くない,と言うことがわかる.
因子寄与率,累積寄与率
2番目の表の「Proportion Var」と「Cumulative Var」はそれぞれ因子寄与率と累積寄与率である.これはVarimax回転の時に有効である.主成分分析の寄与率,累積寄与率とほぼ同じ意味で,共通因子がどれだけデータを説明できているかを表す.(Promax回転場合は,累積寄与率は出ても値に意味はない.寄与率そのものは相対的に扱うことができる)
ちなみにその後の「Proportion Explainded」は「説明率」,「Cumulative Proportion」は「累積説明率」で,合計が1であることから,この場合は寄与率よりもこちらの累積説明率の方が主成分分析に近いイメージ.
Promax回転
今度は共通因子数1と2にそれぞれ,Promax回転を試してみる.
result.fa <-fa(r=df.X, nfactors=1, fm="ml", rotate="promax")
print(result.fa, digits=3, sort=TRUE) Factor Analysis using method = ml
Call: fa(r = df.X, nfactors = 1, rotate = "promax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
V ML1 h2 u2 com
平均雲量 5 0.998 0.995 0.00498 1
日照時間 2 -0.976 0.953 0.04741 1
平均風速 3 0.853 0.727 0.27305 1
降水量の合計 1 0.717 0.515 0.48520 1
平均湿度 4 0.713 0.508 0.49165 1
ML1
SS loadings 3.698
Proportion Var 0.740
Mean item complexity = 1
Test of the hypothesis that 1 factor is sufficient.
The degrees of freedom for the null model are 10 and the objective function was 5.972 with Chi Square of 773.424
The degrees of freedom for the model are 5 and the objective function was 0.306
The root mean square of the residuals (RMSR) is 0.026
The df corrected root mean square of the residuals is 0.037
The harmonic number of observations is 133 with the empirical chi square 1.849 with prob < 0.87
The total number of observations was 133 with Likelihood Chi Square = 39.442 with prob < 1.93e-07
Tucker Lewis Index of factoring reliability = 0.9093
RMSEA index = 0.2316 and the 90 % confidence intervals are 0.1654 0.2972
BIC = 14.99
Fit based upon off diagonal values = 0.999
Measures of factor score adequacy
ML1
Correlation of (regression) scores with factors 0.998
Multiple R square of scores with factors 0.996
Minimum correlation of possible factor scores 0.991Factor Analysis using method = ml
Call: fa(r = df.X, nfactors = 2, rotate = "promax", fm = "ml")
Warning: A Heywood case was detected.
Standardized loadings (pattern matrix) based upon correlation matrix
item ML1 ML2 h2 u2 com
日照時間 2 -1.041 0.059 0.995 0.00497 1.01
平均雲量 5 0.847 0.181 0.978 0.02187 1.09
降水量の合計 1 0.752 -0.021 0.543 0.45739 1.00
平均風速 3 0.673 0.232 0.740 0.26015 1.23
平均湿度 4 0.003 0.880 0.778 0.22222 1.00
ML1 ML2
SS loadings 2.994 1.039
Proportion Var 0.599 0.208
Cumulative Var 0.599 0.807
Proportion Explained 0.742 0.258
Cumulative Proportion 0.742 1.000
With factor correlations of
ML1 ML2
ML1 1.000 0.745
ML2 0.745 1.000
Mean item complexity = 1.1
Test of the hypothesis that 2 factors are sufficient.
The degrees of freedom for the null model are 10 and the objective function was 5.972 with Chi Square of 773.424
The degrees of freedom for the model are 1 and the objective function was 0.02
The root mean square of the residuals (RMSR) is 0.011
The df corrected root mean square of the residuals is 0.033
The harmonic number of observations is 133 with the empirical chi square 0.293 with prob < 0.588
The total number of observations was 133 with Likelihood Chi Square = 2.549 with prob < 0.11
Tucker Lewis Index of factoring reliability = 0.9795
RMSEA index = 0.111 and the 90 % confidence intervals are 0 0.2821
BIC = -2.341
Fit based upon off diagonal values = 1
Measures of factor score adequacy
ML1 ML2
Correlation of (regression) scores with factors 0.998 0.935
Multiple R square of scores with factors 0.996 0.875
Minimum correlation of possible factor scores 0.992 0.749共通因子数2の結果を見ると,共通因子1(ML1)と共通因子2(ML2)の因子負荷量の差が,varimax回転の時に比べ非常に大きい.つまり因子分析が成功したと考えられる.
varimax回転はごく基本的な処理で(直交回転と呼ぶ),Promax回転(斜交回転)の方が性能がいいようだ.
結果の解釈
因子分析で一番重要となのは結果の解釈である.わかりやすいので,Promax回転の共通因子数2の場合を見てみよう.結果を再掲する.
item ML1 ML2 h2 u2 com
日照時間 2 -1.041 0.059 0.995 0.00497 1.01
平均雲量 5 0.847 0.181 0.978 0.02187 1.09
降水量の合計 1 0.752 -0.021 0.543 0.45739 1.00
平均風速 3 0.673 0.232 0.740 0.26015 1.23
平均湿度 4 0.003 0.880 0.778 0.22222 1.00共通因子1(ML1)は,日照時間の因子負荷量が1or-1に近く,かつ共通性が非常に高いことから,日照時間に強く影響を与えている.同じように(日照時間ほどではないが)平均雲量と降水量の合計,平均風速に大きく影響を与えている.
ここで「1月のデータ」だったことを思い出そう.太平洋側と日本海側の都市の冬の気候は,日本海側が基本的に荒天であり,太平洋側は基本的に晴天である.日本海側は冬の日照時間がほとんどなく(日照時間が0からほぼ動かない,つまり負の影響が出る,また,雲の量が多い),かつ雪が降る(降水量はプラスの方向に動く,つまり正の方向に影響が出る)と考えると,共通因子1(ML1)は明確に,「太平洋側の都市かどうか」を表していると言えるのではないだろうか.
つまり,この共通因子1は,前回の二項分類で使った太平洋側日本海側ダミー変数そのものということができる.
風速は,日照時間ほどではないが,同じく影響を太平洋側日本海側に大きく与えている.
平均湿度に関してはどうだろう? 共通因子1つまり太平洋側か日本海側かにはほぼ影響を受けていないことがわかる.平均湿度に影響を与えている共通因子2はどうやら別の要素らしい.元データを見返しながら,観測値の4都市の気候を分析し,この共通因子2に名前をつけてみよう.