今回も「気温以外のデータ」を使って,さらに線形分類の時よりも観測データを多くして,太平洋側の都市と日本海側の都市を比較してみる.
因子分析
因子分析とは,観測された変数の「原因となっている何らかの変数」が隠れて存在する(潜在変数)と考え,その変数を探す分析のことである.
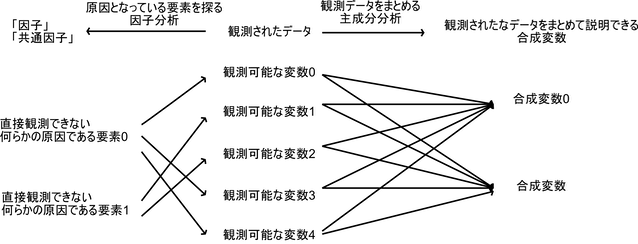
例えば太平洋側の都市と日本海側の都市では冬の気候に大きな違いがあるが,観測データには何らかの「観測可能なデータの違い」があり,その観測可能なデータから「原因」である「気候の違い」を,「なるべく少ない要素」で表現できるように探すことが目的である.
「どちらか側の海」というのは根本的な原因であるダミー変数だが,ダミー変数を直接出せるほど因子分析は優れてはいないので,潜在変数はスカラ値であることがほとんどである.
次元圧縮としても使えてしまうため,主成分分析と混同されることがあるが,因子分析と主成分分析は考え方が逆である.
因子分析は「観測可能なデータから,観測データの原因となっている少数の要素(因子,潜在変数)があると仮定して,それを推測する」
主成分分析は「観測可能なデータから,少数で多くの観測データを上手く表現することができる少数の合成変数を作成する」
である.
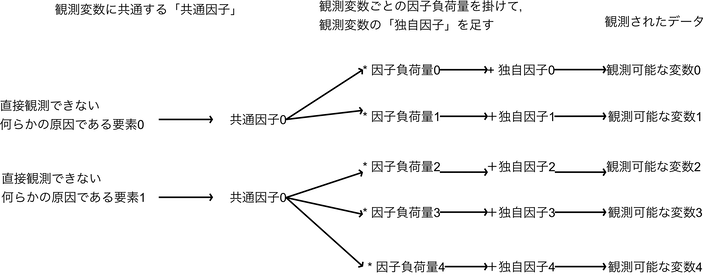
実際には「共通因子」に,どのぐらい共通因子が占める割合が大きいかの「因子負荷量」を掛け,その変数の独自の要素である「独自因子」を足したものが,観測データである.
因子分析の特徴として,因子の数がいくつあるかを与えなければならない.因子分析の手法は多く提唱されており色々な組み合わせがあるが,「回転法」が直交法 - Varimax回転の時に因子数の指標となるのが「因子負荷量」である.
因子負荷量は,その仮定した因子がどのぐらい各観測変数に影響を与えているか(正確には各観測変数と各因子の相関係数,つまり連動して動いているか)を見るもので,因子負荷量が各変数において各因子間の違いが大きければ大きいほど,その仮定した因子数は適切である,と考える.(相関係数なので-1から1の間に収まる.0の時は「観測変数とその因子は全く連動していない」ということになる.)
具体的には,「各変数の各因子に対する因子負荷量を見て,一つの因子のみ1(もしくは-1)に近く,他の因子は0に近い」場合には,その因子の選定は適切である,となる.
データの取得と加工
例によって,気象庁オープンデータのページから,
都市は,秋田県→秋田市,岩手県→宮古市,山形県→酒田市,宮城県→石巻市,の順で,それぞれ選択.
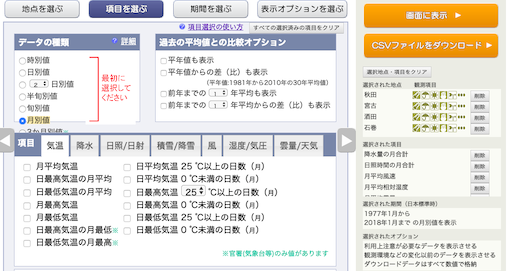
今回も「気温以外のデータ」なので,気温は選択しない.
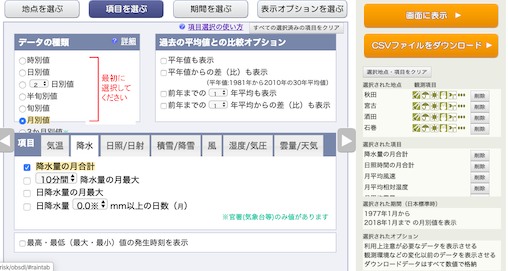
月別の値を選択し,降水量の月合計,
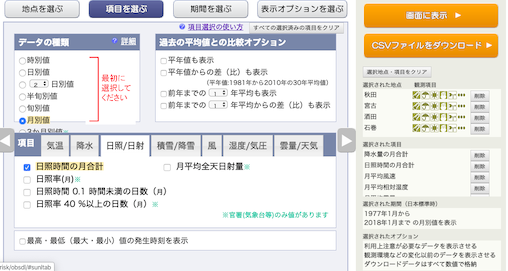
日照時間の月合計,
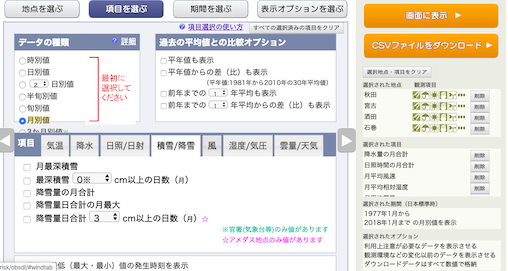
月平均風速,
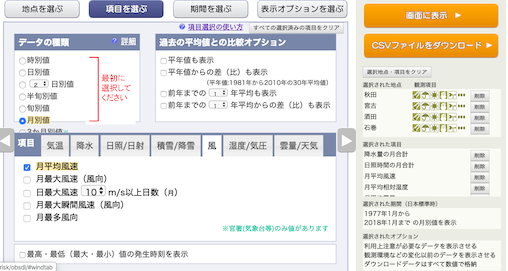
湿度/気圧の月平均蒸気圧,を選択し,
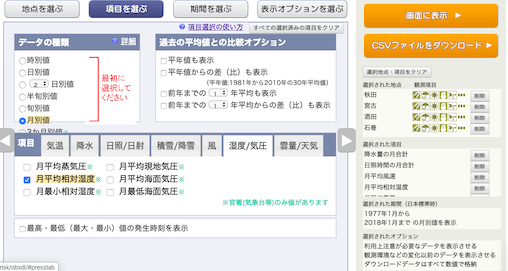
平均雲量,を選択し,
1977年〜2018年の「1月」のデータをダウンロードする.
表示オプションはデフォルト.地点の順番と,項目の順番を確認すること.
実際のCSVファイルは,この通りである.
Googleスプレッドシートに読み込む.スタック形式のデータにする.
いつものように不要な行と列を削除.年月の列も使わないので削除.
一番左の列を選択肢,右クリック→「1列左に挿入」で,「観測地点」を記入する列を挿入
作られた列の冒頭に「観測地点」の列名を記入.
観測地点列に「秋田」を入力.
宮古の観測データを洗濯して,右クリック→「切り取り」
秋田の下に貼り付ける.一番左は「観測地点」列なので,列を間違わないこと.
観測地点列に「宮古」を入力.
同じく酒田のデータを作成.
同じく石巻のデータを作成.
列名を短く整える.
これまでと同じ様に,ファイル→ウェブに公開.
CSV形式でウェブに公開してURLをコピーしておく.
因子分析の実行・共通因子数決定の流れ
factor-analyzerというライブラリパッケージが高機能で使いやすいので,これを使う.
# 高機能因子分析パッケージ
!pip install factor-analyzer
因子分析は,最初に「幾つの共通因子があるか」を与えなければならない.共通因子数を変えながら探索的に共通因子数を探ることを「探索的因子分析」と呼ぶ.これを行なっていく.
まず一番最初,観測値の数,つまり変数の数は5なので,1つ減らした4で因子分析を実行してみる.
データの加工の過程で気づいたかもしれないが,平均雲量は後半ほぼ欠損している.気象庁の観測態勢が変更になったと思われるが,欠損値を削除しなければならない.とは言っても因子分析の間数事態に欠損値をどうするかのimpute=オプションがあり,dropを与えることで,勝手に行ごと削除してくれる.
使用する手法は,ごく一般的な「最尤法」を意味するmethod='ml',回転法はとりあえず基本である「Varimax法」rotation='varimax'を指定する.
from factor_analyzer import FactorAnalyzer
import seaborn as sns
# 何因子だと考えるか
# とりあえず最初は多めに
n_factors=4
fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
# method: 使用する手法
# minres (ミンレス法)
# ml (最尤法)
# principal(主因子法)
# rotation 回転法
# varimax (バリマックス回転) 直交法
# promax (プロマックス回転) 斜交法
# oblique (斜め回転)
# impute 欠損値をどうするか
# drop: 削除
x_label = ['降水量の合計', '日照時間', '平均風速', '平均湿度', '平均雲量']
# データにフィットさせる
# 因子分析の対象にするのは5観測変数であり,観測地点は使わないので0列目以外を抽出
fa_model.fit(df.iloc[:, 1:])
# 因子負荷量はloadings_プロパティで読み出せるので,結果のDataFrameを作る
# 因子負荷量:因子と観測変数の間の関係性の強弱のこと
# 行名(index)として,この列名のラベルを用いて,DataFrameを作る
df_result = pd.DataFrame(fa_model.loadings_, index=x_label)
# 因子負荷量の行列を色分けして表示
cm = sns.light_palette('red', as_cmap=True)
# セルの最後に実行すること.df.head()と同じく,printしても色分けされない
df_result.style.background_gradient(cmap=cm)
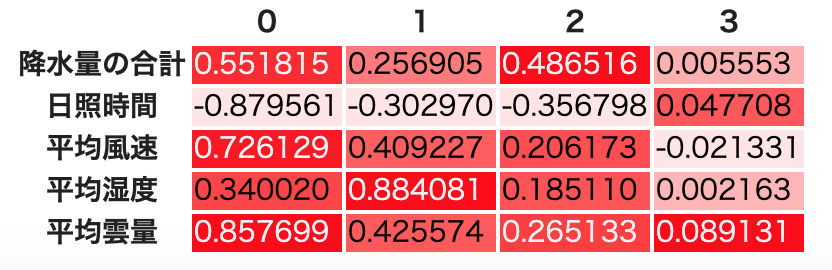
Varimax回転をPromax回転に変えるなどして,回転方法によって結果が変わることを確かめる.(ただしPromax回転の場合因子負荷量に意味はないので参考程度に)
ここで表示されたのは,各共通因子と各観測変数の間の「因子負荷量」である.因子負荷量は「その共通因子が変数つまり観測された値にどれだけ影響を与えているか」の値で,-1から1の間を取る.
1つの観測変数に対する因子負荷量が各因子間(ここでは列0〜烈3の間)で大きく差がある(理想的なのは,1観測変数に対して,1因子だけ1もしくは-1に近く,他の因子では0に近い)と,うまく因子分析が機能し共通因子にまとめられたことを表し,逆に.1つの観測変数に対して因子負荷量の因子間の差が小さい場合は因子分析がうまくいかなかったことを示している.
降水量の合計は,どの共通因子でも因子負荷量に大した差がない.特に因子0と因子2は非常に近い値になっている.したがって共通因子数に4を仮定するのは具合が悪い,ということになる.
次に「累積寄与率」を見てみる.get_factor_varience()[2]に入っている.
# Varimax回転の場合の因子数4での累積寄与率
factor_index = list([])
for i in range(n_factors):
factor_index.append('共通因子' + str(i))
df_cumulative_variance = pd.DataFrame(fa_model.get_factor_variance()[2], index=factor_index)
df_cumulative_variance.style.background_gradient(cmap=cm)

累積寄与率は,Varimax回転の時に有効である.主成分分析の寄与率,累積寄与率とほぼ同じ意味で,共通因子がどれだけデータを説明できているかを表す.(Promax回転場合は,累積寄与率は出ても値に意味はない.ただし寄与率そのものは相対的に扱うことができる)
共通因子数3で85.1%を説明できており,共通因子数4になってもたいして変わらないことから,やはり共通因子数4を使うのは具合が良くないことが示された.
散布図で見てみよう.因子数4の時の,観測値を共通因子に変換し,その散布図を描く.共通因子数4なのでそれぞれの共通因子を軸にとると,3*2で6つのグラフを描くことができる.
# 因子分析関数は欠損地のある行を削除してくれたが,グラフで描く時には関係ないので,
# まず欠損値のある行を削除して,再代入しておく
df = df.dropna(how='any')
# 因子分析の結果を使って,観測値を共通因子の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df.iloc[:, 1:]))
num_of_row = df.values.shape[0]
# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
ishinomaki = list([])
for i in range(num_of_row):
if df.values[i][0] == '秋田':
akita.append(factors_df.iloc[i, :])
elif df.values[i][0] == '宮古':
miyako.append(factors_df.iloc[i, :])
elif df.values[i][0] == '酒田':
sakata.append(factors_df.iloc[i, :])
else:
ishinomaki.append(factors_df.iloc[i, :])
df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_ishinomaki = pd.DataFrame(ishinomaki)
import matplotlib.pyplot as plt
plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 0], df_ishinomaki.iloc[:, 1], label='Ishinomaki')
plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()
plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 2], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 2], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 2], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 0], df_ishinomaki.iloc[:, 2], label='Ishinomaki')
plt.xlabel('Factor0')
plt.ylabel('Factor2')
plt.legend()
plt.show()
plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 0], df_ishinomaki.iloc[:, 3], label='Ishinomakii')
plt.xlabel('Factor0')
plt.ylabel('Factor3')
plt.legend()
plt.show()
plt.scatter(df_akita.iloc[:, 1], df_akita.iloc[:, 2], label='Akita')
plt.scatter(df_sakata.iloc[:, 1], df_sakata.iloc[:, 2], label='Sakata')
plt.scatter(df_miyako.iloc[:, 1], df_miyako.iloc[:, 2], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 1], df_ishinomaki.iloc[:, 2], label='Ishinomaki')
plt.xlabel('Factor1')
plt.ylabel('Factor2')
plt.legend()
plt.show()
plt.scatter(df_akita.iloc[:, 1], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 1], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 1], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 1], df_ishinomaki.iloc[:, 3], label='Ishinomaki')
plt.xlabel('Factor1')
plt.ylabel('Factor3')
plt.legend()
plt.show()
plt.scatter(df_akita.iloc[:, 2], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 2], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 2], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 2], df_ishinomaki.iloc[:, 3], label='石巻')
plt.xlabel('Factor2')
plt.ylabel('Factor3')
plt.legend()
plt.show()
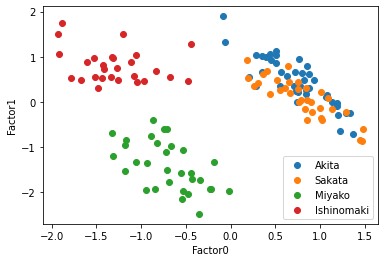
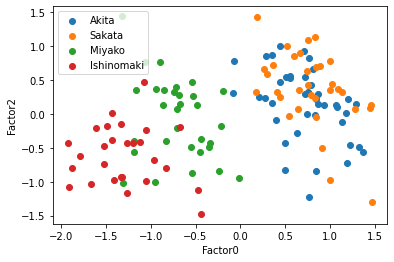
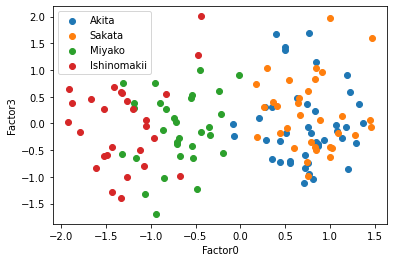
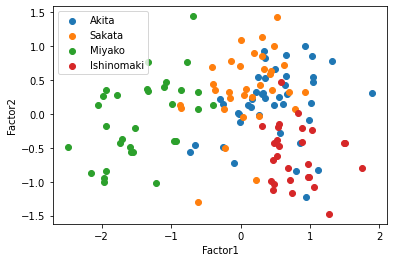
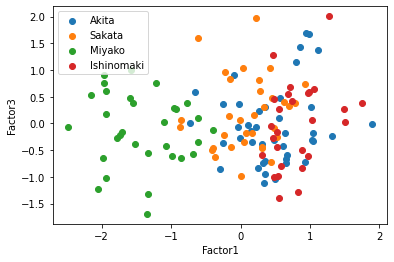
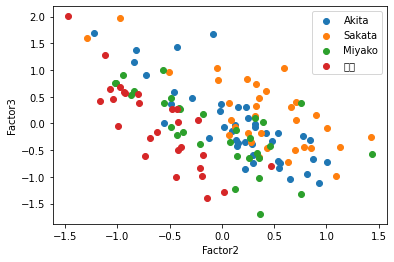
この散布図を見ると,共通因子0で太平洋側と日本海側を直線で分けられるように見える,因子負荷量を考えると,もっと因子数が少ない方がいいかもしれない.そこで因子数3と2についてもまったく同じように行っていく.
# 共通因子数3の場合
n_factors=3
fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
fa_model.fit(df.iloc[:, 1:])
df_result = pd.DataFrame(fa_model.loadings_, index=x_label)
cm = sns.light_palette('red', as_cmap=True)
df_result.style.background_gradient(cmap=cm)
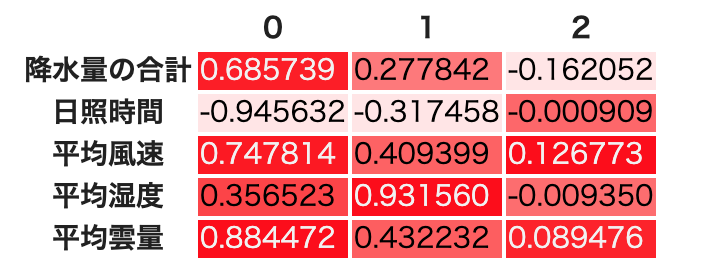
# Varimax回転の時の共通因子数3での累積寄与率
factor_index = list([])
for i in range(n_factors):
factor_index.append('共通因子' + str(i))
df_cumulative_variance = pd.DataFrame(fa_model.get_factor_variance()[2], index=factor_index)
df_cumulative_variance.style.background_gradient(cmap=cm)

因子負荷量は,そこまで綺麗に分離はしていない.しかし累積寄与率は上がっているので,共通因子数3の方が4よりもいいようだ.
共通因子数2の時は,
# 共通因子数3の場合
n_factors=2
fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
fa_model.fit(df.iloc[:, 1:])
df_result = pd.DataFrame(fa_model.loadings_, index=x_label)
cm = sns.light_palette('red', as_cmap=True)
df_result.style.background_gradient(cmap=cm)
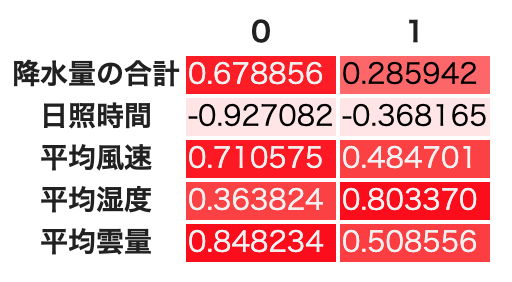
# Varimax回転の時の共通因子数2での累積寄与率
factor_index = list([])
for i in range(n_factors):
factor_index.append('共通因子' + str(i))
df_cumulative_variance = pd.DataFrame(fa_model.get_factor_variance()[2], index=factor_index)
df_cumulative_variance.style.background_gradient(cmap=cm)
因子数2の時,因子負荷量が因子間でそれなりに大きく離れている.降水量,日照時間,雲量は因子0に,風速と湿度は因子1にそれぞれ大きな影響を受けている.
共通因子数1も考えられるが,因子数を3以下にする場合因子数2で良さそうだ(共通因子数1でもいいかもしれない).確かめるために散布図を描いてみる.
# 因子分析の結果を使って,観測値を共通因子の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df.iloc[:, 1:]))
num_of_row = df.values.shape[0]
# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
ishinomaki = list([])
for i in range(num_of_row):
if df.values[i][0] == '秋田':
akita.append(factors_df.iloc[i, :])
elif df.values[i][0] == '宮古':
miyako.append(factors_df.iloc[i, :])
elif df.values[i][0] == '酒田':
sakata.append(factors_df.iloc[i, :])
else:
ishinomaki.append(factors_df.iloc[i, :])
df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_ishinomaki = pd.DataFrame(ishinomaki)
import matplotlib.pyplot as plt
plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 0], df_ishinomaki.iloc[:, 1], label='Ishinomaki')
plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()
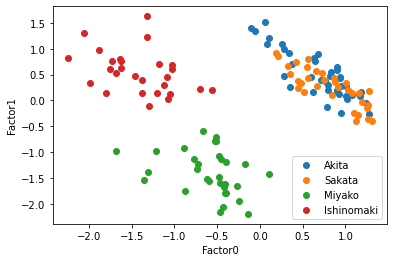
秋田と酒田はやはり分けることができていないが,宮古と石巻は共通因子1によって綺麗に分離しており,共通因子1の軸では酒田・秋田・石巻が同じような共通因子の値を持つことが示されている.この4都市に関して共通因子が2つ存在すると考えるのは妥当そうだ.
これまではVarimax回転だったが,Promax回転をしてみよう.前述の通りPromax回転では因子負荷量が絶対的な値ではなくなるが,より明確に分離して見えるようになる.
# 共通因子数2のPromax回転の場合
n_factors=2
fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='promax', impute='drop')
fa_model.fit(df.iloc[:, 1:])
df_result = pd.DataFrame(fa_model.loadings_, index=x_label)
cm = sns.light_palette('red', as_cmap=True)
df_result.style.background_gradient(cmap=cm)
# 共通因子数2のPromax回転の散布図
# 因子分析の結果を使って,観測値を共通因子の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df.iloc[:, 1:]))
num_of_row = df.values.shape[0]
# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
ishinomaki = list([])
for i in range(num_of_row):
if df.values[i][0] == '秋田':
akita.append(factors_df.iloc[i, :])
elif df.values[i][0] == '宮古':
miyako.append(factors_df.iloc[i, :])
elif df.values[i][0] == '酒田':
sakata.append(factors_df.iloc[i, :])
else:
ishinomaki.append(factors_df.iloc[i, :])
df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_ishinomaki = pd.DataFrame(ishinomaki)
plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_ishinomaki.iloc[:, 0], df_ishinomaki.iloc[:, 1], label='Ishinomaki')
plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()
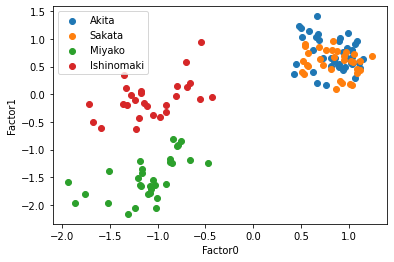
Varimax開店の時より,より明確にクラスターが形成されている.
結果の解釈
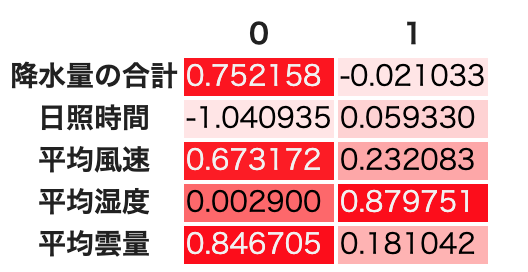
因子分析で一番重要となのは結果の解釈である.わかりやすいので,Promax回転の共通因子数2の場合を見てみよう.結果を再掲する.

共通因子0は,日照時間の因子負荷量が1or-1に近く,日照時間に強く影響を与えている.同じように(日照時間ほどではないが)平均雲量と降水量の合計,平均風速に大きく影響を与えている.
ここで「1月のデータ」だったことを思い出そう.太平洋側と日本海側の都市の冬の気候は,日本海側が基本的に荒天であり,太平洋側は基本的に晴天である.日本海側は冬の日照時間がほとんどなく(日照時間が0からほぼ動かない,つまり負の影響が出る,また,雲の量が多い),かつ雪が降る(降水量はプラスの方向に動く,つまり正の方向に影響が出る)と考えると,共通因子0は明確に,「太平洋側の都市かどうか」を表していると言えるのではないだろうか.
つまり,この共通因子0は,前回の二項分類で使った太平洋側日本海側ダミー変数そのものということができる.
風速は,日照時間ほどではないが,同じく影響を太平洋側日本海側に大きく与えている.
平均湿度に関してはどうだろう? 共通因子0つまり太平洋側か日本海側かにはほぼ影響を受けていないことがわかる.平均湿度に影響を与えている共通因子1はどうやら別の要素らしい.元データを見返しながら,観測値の4都市の気候を分析し,この共通因子1に名前をつけてみよう.