こーひーをぶんなぐれ！ - Work

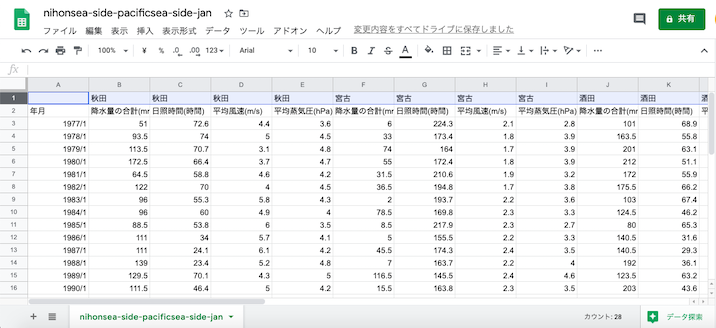
本項でもGoogle Colaboratoryを使用する．（もちろんファイル読み込みの部分以外はJupyter Notebookでもよいし，一気にPythonのソースコードをまとめて書いて実行しても問題はない）

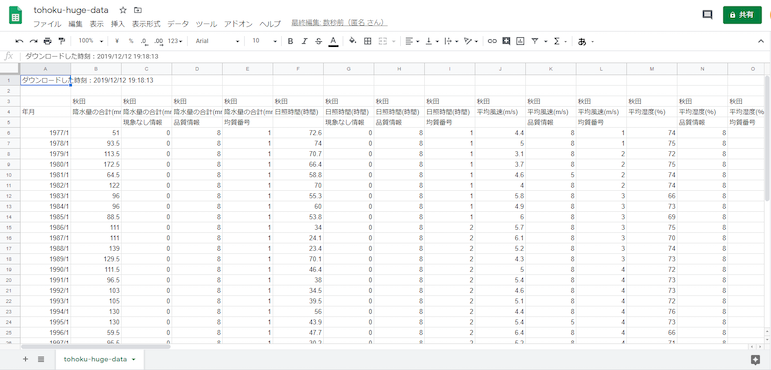
今回も「気温以外のデータ」を使って，さらに線形分類の時よりも観測データを多くして，太平洋側の都市と日本海側の都市を比較してみる．

例によって，気象庁オープンデータのページから，

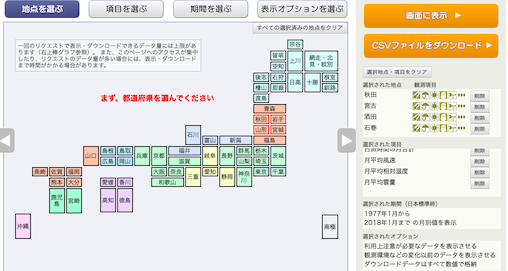
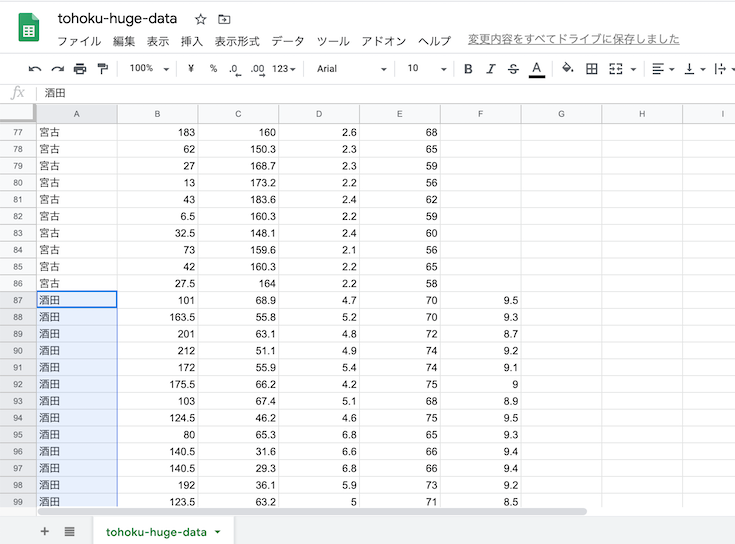
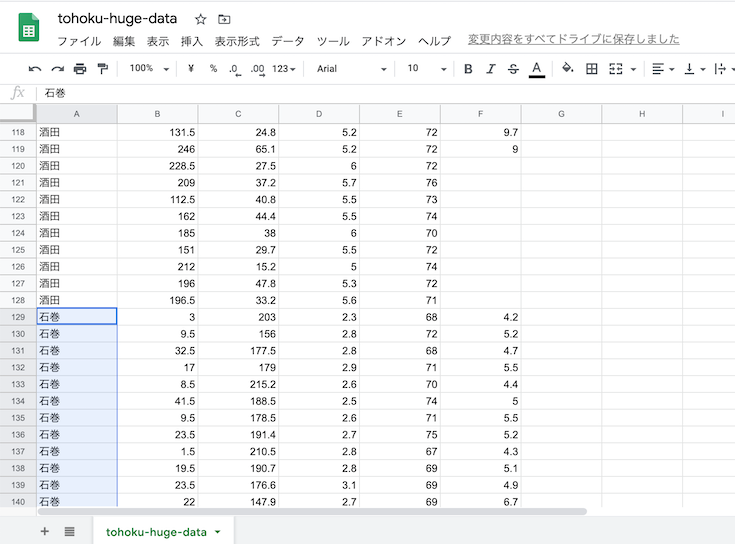
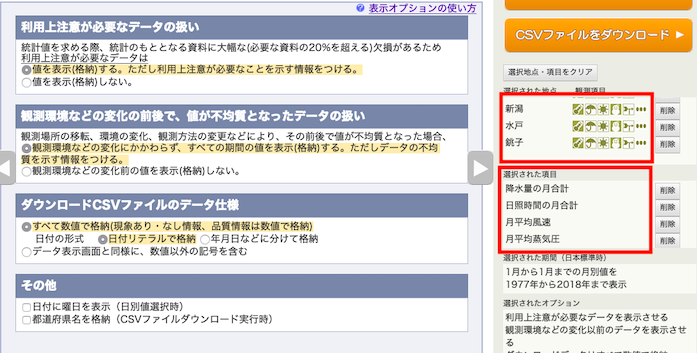
都市は，秋田県→秋田市，岩手県→宮古市，山形県→酒田市，宮城県→石巻市，の順で，それぞれ選択．

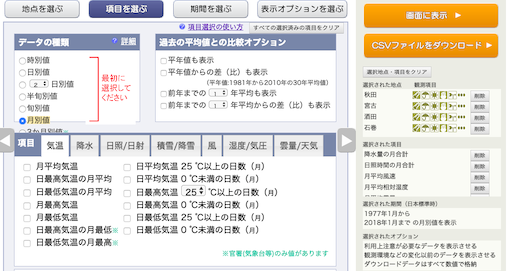
今回も「気温以外のデータ」なので，気温は選択しない．

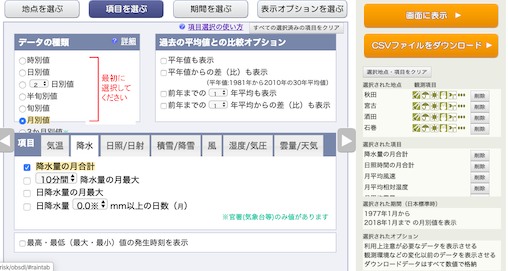
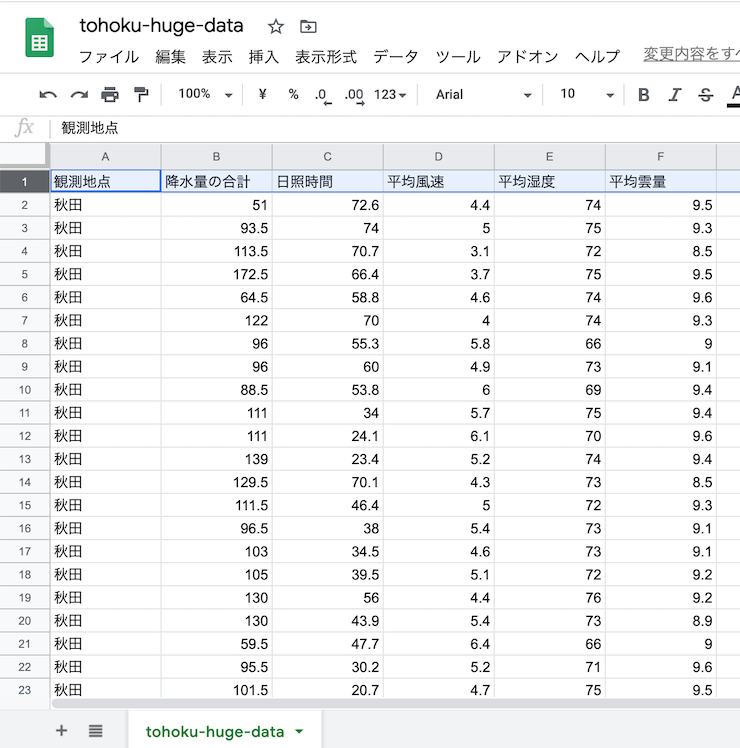
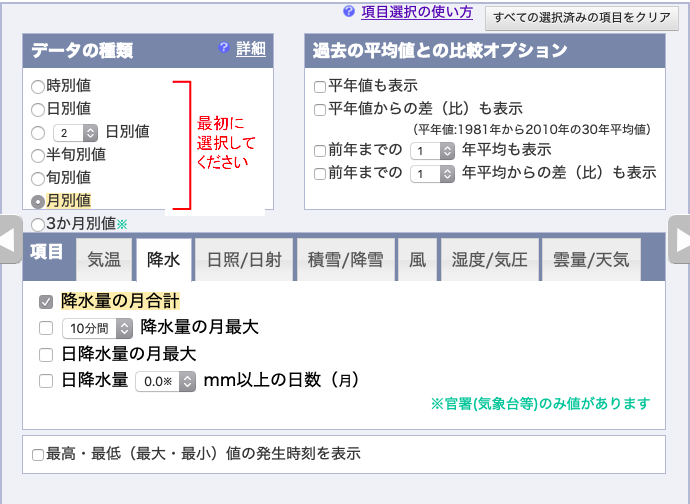
月別の値を選択し，降水量の月合計，

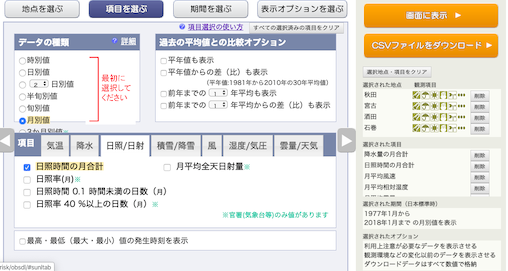
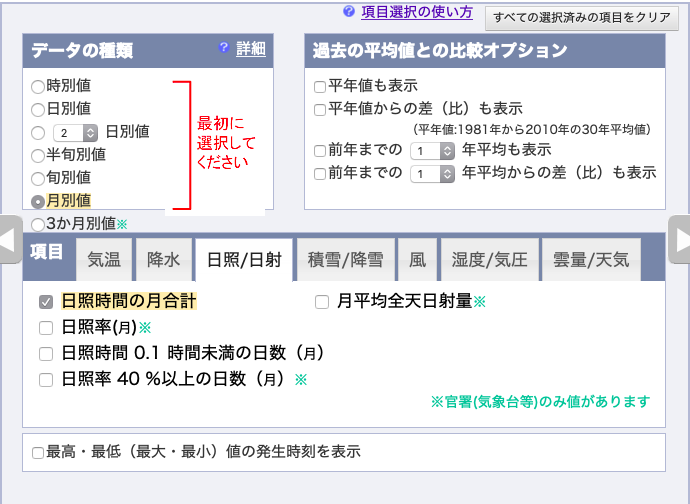
日照時間の月合計，

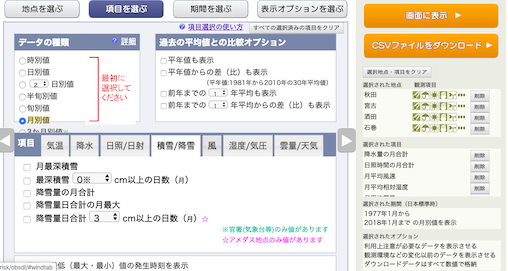
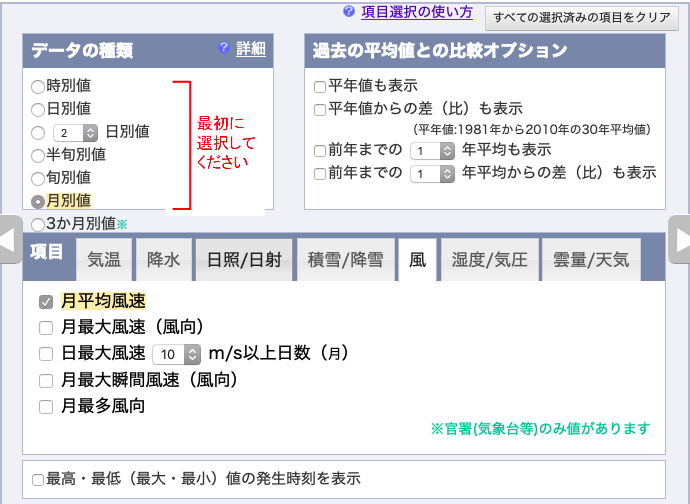
月平均風速，

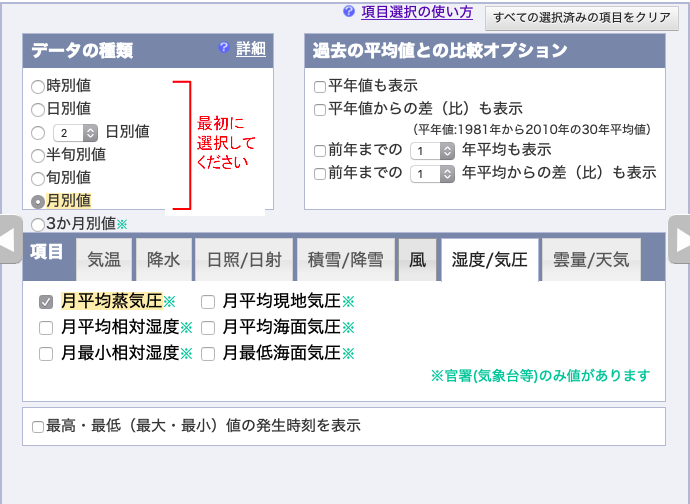
湿度/気圧の月平均蒸気圧，を選択し，

平均雲量，を選択し，

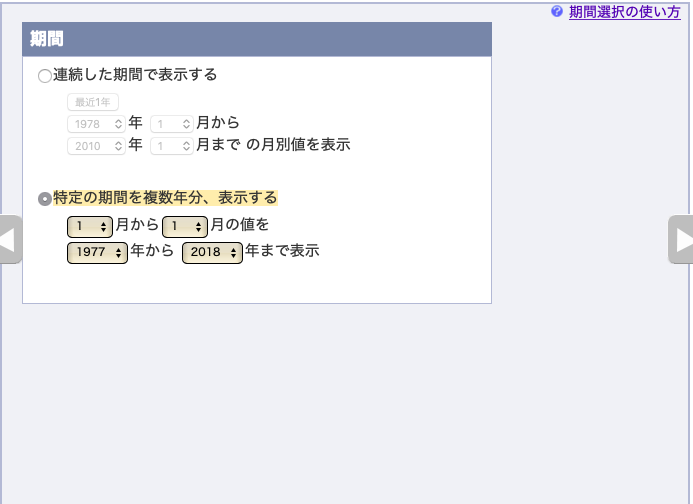
1977年〜2018年の「1月」のデータをダウンロードする．

表示オプションはデフォルト．地点の順番と，項目の順番を確認すること．

実際のCSVファイルは，この通りである．

因子分析

因子分析とは，観測された変数の「原因となっている何らかの変数」が隠れて存在する（潜在変数）と考え，その変数を探す分析のことである．

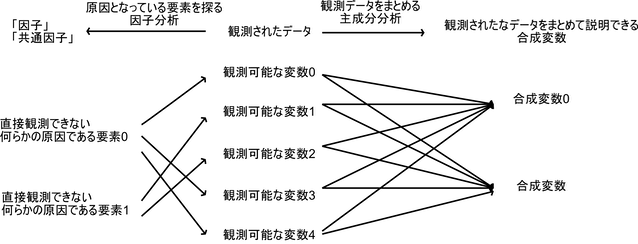
例えば太平洋側の都市と日本海側の都市では冬の気候に大きな違いがあるが，観測データには何らかの「観測可能なデータの違い」があり，その観測可能なデータから「原因」である「気候の違い」を，「なるべく少ない要素」で表現できるように探すことが目的である．

「どちらか側の海」というのは根本的な原因であるダミー変数だが，ダミー変数を直接出せるほど因子分析は優れてはいないので，潜在変数はスカラ値であることがほとんどである．

次元圧縮としても使えてしまうため，主成分分析と混同されることがあるが，因子分析と主成分分析は考え方が逆である．

因子分析は「観測可能なデータから，観測データの原因となっている少数の要素（因子，潜在変数）があると仮定して，それを推測する」

主成分分析は「観測可能なデータから，少数で多くの観測データを上手く表現することができる少数の合成変数を作成する」

である．

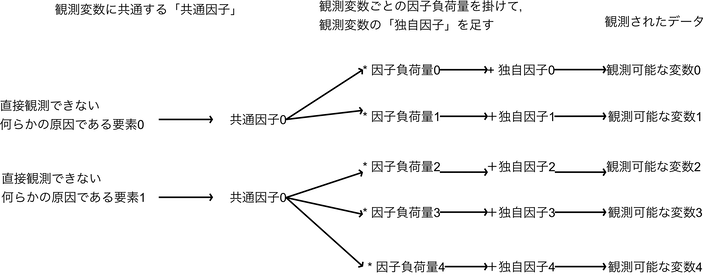
実際には「共通因子」に，どのぐらい共通因子が占める割合が大きいかの「因子負荷量」を掛け，その変数の独自の要素である「独自因子」を足したものが，観測データである．

因子分析の特徴として，因子の数がいくつあるかを与えなければならない．因子分析の手法は多く提唱されており色々な組み合わせがあるが，「回転法」が直交法 - Varimax回転の時に因子数の指標となるのが「因子負荷量」である．

因子負荷量は，その仮定した因子がどのぐらい各観測変数に影響を与えているか（正確には各観測変数と各因子の相関係数，つまり連動して動いているか）を見るもので，因子負荷量が各変数において各因子間の違いが大きければ大きいほど，その仮定した因子数は適切である，と考える．（相関係数なので-1から1の間に収まる．0の時は「観測変数とその因子は全く連動していない」ということになる．）

具体的には，「各変数の各因子に対する因子負荷量を見て，一つの因子のみ1（もしくは-1）に近く，他の因子は0に近い」場合には，その因子の選定は適切である，となる．

コード例

1つ目のセル．いつもと同じくCSVをColabへ読み込む．

from google.colab import files
uploaded = files.upload()

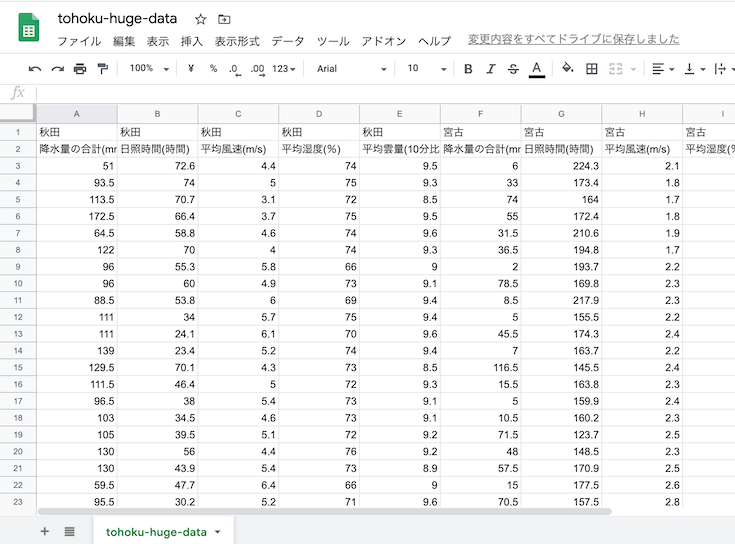
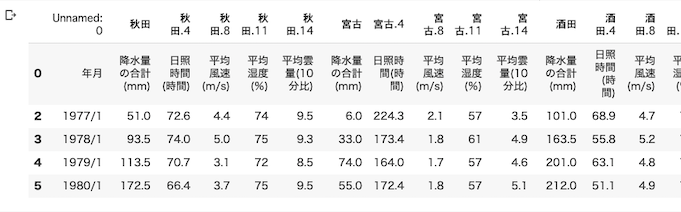
2つ目のセル．品質情報などの列が不要なので削除．

# CSVを整えてDataFrameにする
import numpy as np
import pandas as pd
from pandas import Series, DataFrame

df = pd.read_csv('tohoku-huge-data.csv', encoding='SHIFT-JIS', header=1)

# 抜き出す
for a_column in ['秋田', '宮古', '酒田', '石巻']:
  # それぞれ
  # 降水量の合計(mm),降水量の合計(mm),降水量の合計(mm),降水量の合計(mm),日照時間(時間),日照時間(時間),日照時間(時間),日照時間(時間),平均風速(m/s),平均風速(m/s),平均風速(m/s),平均湿度(％),平均湿度(％),平均湿度(％),平均雲量(10分比),平均雲量(10分比),平均雲量(10分比)
  # で並んでいて，一つの地点につき，
  # (空),現象なし情報,品質情報,均質番号,(空),現象なし情報,品質情報,均質番号,(空),品質情報,均質番号,(空),品質情報,均質番号,(空),品質情報,均質番号
  # の順に並んでいる
  # の(空)以外の場所が余計なので，削除
  for i in range(1, 17, 1):
    # 落とす列の列番号を指定(0~)
    if i in [1, 2, 3, 5, 6, 7, 9, 10, 12, 13, 15, 16]:
      df = df.drop(a_column + '.' + str(i), axis=1)

df = df.drop(1)

# DataFrameの中に欠損値がある場合は，0.0を代わりに入れておく
df = df.fillna(0)
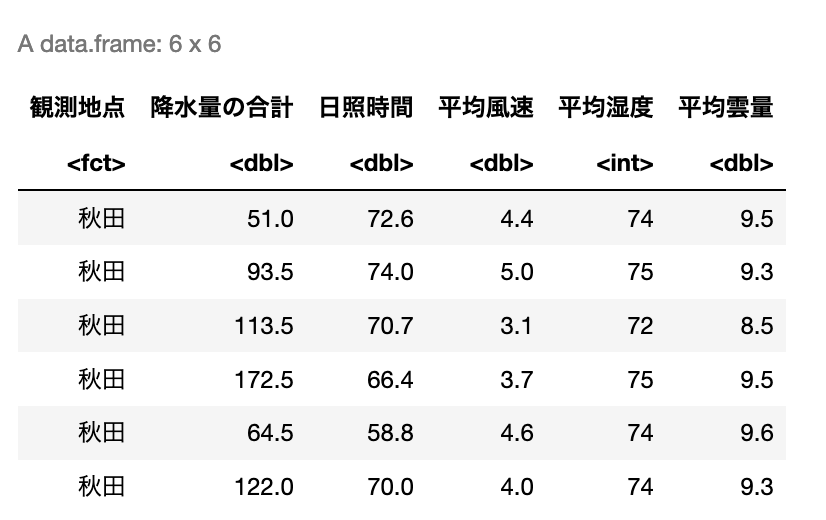
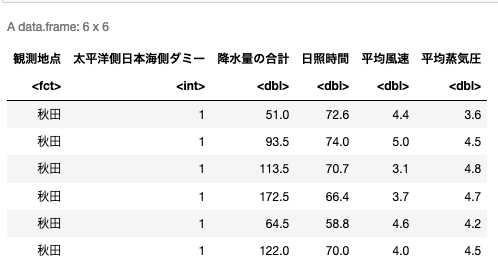
df.head()

2つ目のセルの結果は以下の通り

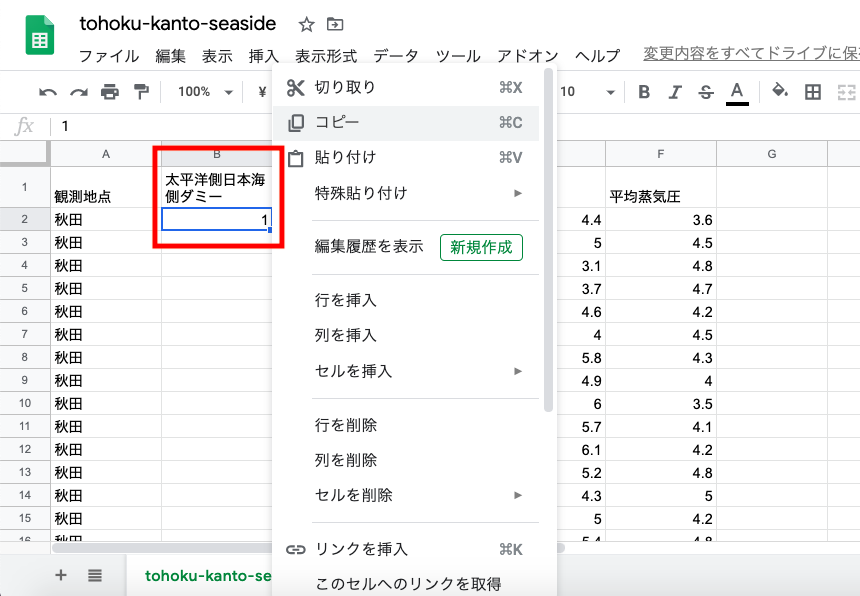
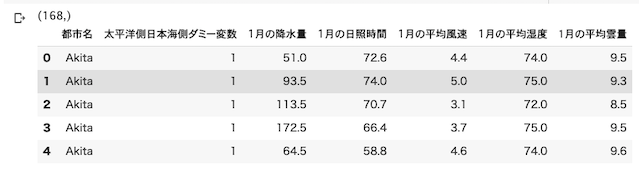
3つ目のセル．都市名，ダミー変数を入れて，各都市のデータの列を繋いで，一つのデータフレームにする．

# グラフ表示するためにローマ字ラベルを作っておく
#np.arrayはenumerateでは回せないので，　listのままにしておく
city_label_list = (['Akita', 'Miyako', 'Sakata', 'Ishinomaki'])

# その要素の有無で0と1の2値で表現される変数を「ダミー変数」と呼ぶ
# 0, 1, 2, 3...などの状態が複数あり，かつその数字が大小の意味を持ってない場合は，カテゴリ変数と呼ぶ
# カテゴリ変数は判別問題などで扱えないので，
# カテゴリ変数で表現している内容を，要素に分けて，要素の有無で表現，つまり複数のダミー変数に直す

# 今回は太平洋側と日本海側の2値なので，ダミー変数：太平洋側が0, 日本海側が1
sea_side_label = np.array([1, 0, 1, 0])

# 選んだ都市の
# precipitation: 1月の降水量
# daylight_hours: 1月の日照時間
# average_wind_speed: 1月の平均風速
# average_humidity: 1月の平均湿度
# amounts_clouds: １月の平均雲量

# として，それぞれ42年分*太平洋側，日本海側の2年ずつを，1つ配列としてくっつける

# 42年分のラベルを繋げておく　(42年分*全部の都市)
city_label_in_repeat = np.repeat(city_label_list, 42)
sea_side_label_in_repeat = np.repeat(sea_side_label, 42)
print(sea_side_label_in_repeat.shape)

# データをつなげる
# まず最初に空の配列を作っておいて，
precipitation = np.array([], dtype=np.float)
daylight_hours = np.array([], dtype=np.float)
average_wind_speed = np.array([], dtype=np.float)
average_humidity = np.array([], dtype=np.float)
amounts_clouds = np.array([], dtype=np.float)

# 選んだ都市の，1月の平均風速，1月の日照時間，1月の平均湿度，1月の降水量を
# それぞれ1つの配列につなぐ
for i, a_city in enumerate(city_label_list): 
  precipitation = np.concatenate((precipitation, df.iloc[1:, 1+(i*5)]))
  daylight_hours = np.concatenate((daylight_hours, df.iloc[1:, 1+(i*5)+1]))
  average_wind_speed = np.concatenate((average_wind_speed, df.iloc[1:, 1+(i*5)+2]))
  average_humidity = np.concatenate((average_humidity, df.iloc[1:, 1+(i*5)+3]))
  amounts_clouds = np.concatenate((amounts_clouds, df.iloc[1:, 1+(i*5)+4]))

# vstackで重ねて，配列の次元を入れ替えて，DataFrameにしておく
df_sea_side_city = pd.DataFrame(np.vstack([city_label_in_repeat, sea_side_label_in_repeat, precipitation.astype(np.float), daylight_hours.astype(np.float), average_wind_speed.astype(np.float), average_humidity.astype(np.float), amounts_clouds.astype(np.float)]).transpose())
# DataFrameの列名をつけておく
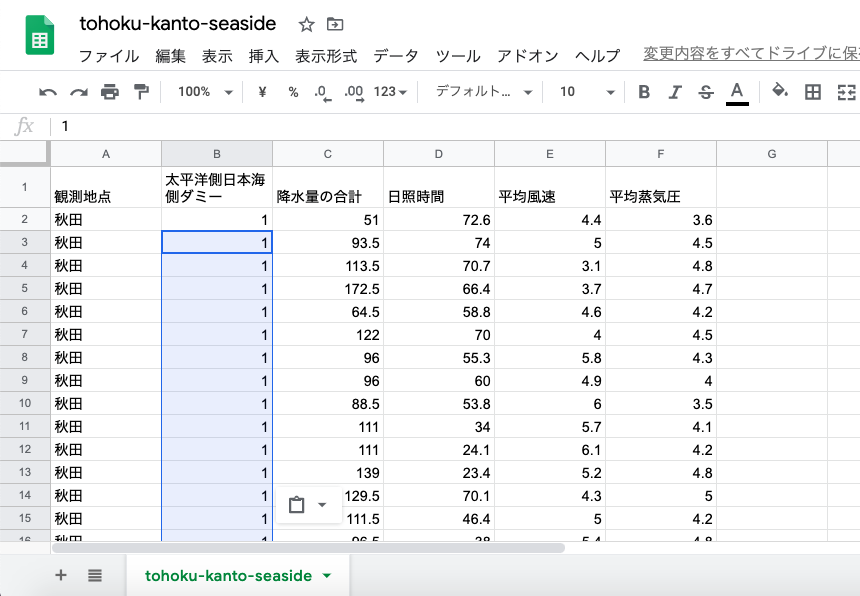
df_sea_side_city = df_sea_side_city.rename(columns={0:'都市名', 1:'太平洋側日本海側ダミー変数', 2:'1月の降水量', 3:'1月の日照時間', 4:'1月の平均風速', 5:'1月の平均湿度', 6:'１月の平均雲量'})
# DataFrameの冒頭を確認
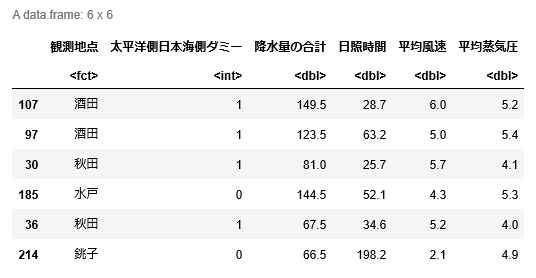
df_sea_side_city.head()

3つ目のセルの結果は以下の通り

4つ目のセル．因子分析のパッケージをインストールする．

# 高機能因子分析パッケージ
!pip install factor-analyzer

5つ目のセル．変数の数が5つなので，とりあえず因子数4で因数分解をして，因子負荷量を算出してみる．

各共通因子と各観測変数の間の「因子負荷量」である．因子負荷量は「その因子が変数にどれだけ影響を与えているか」の値で，-1から1の間を取る．

1つの観測変数に対する因子負荷量が各因子間（ここではML1とML2~4の間）で大きく差がある（典型的なのは，1観測変数に対して，1因子だけ1もしくは-1に近く，他の因子では0に近い）と，うまく因子分析が機能し共通因子にまとめられたことを表し，逆に．1つの観測変数に対して因子負荷量の因子間の差が小さい場合は因子分析がうまくいかなかったことを示している．

# 因子分析
# 観測されたデータ（説明変数）が大量の次元を持ち，
# かつ説明変数感の相関係数が高い場合，
# 因果のルート側に数が少ない潜在変数Latent Variable（因子 Factor）が存在することにより，
# 観測データ = 説明変数が生み出されているという考え方

# 回帰や分類の前処理に使う場合の目的は，次元圧縮なので主成分分析と同じに思えるが，
# 因子分析は，観測データ（説明変数）を潜在変数の組み合わせによる合成量として捉え，その潜在変数を求める
# つまり考え方は主成分分析の逆である．

# 次元圧縮を目的としている場合，次元数を与えられるのは有利だが，
# 機械学習目的ではなく，分析目的の場合，
# 潜在変数の数，すなわち次元数を最初に与えなければならないことは，欠点でもある

# 次元圧縮した状態でグラフ等をみて，これは何の因子なのか，因子が妥当かどうか，を
# 分析者が検討しなければならい

from factor_analyzer import FactorAnalyzer
import seaborn as sns

# 何因子だと考えるか
# とりあえず最初は多めに
n_factors=4


fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
# method: 使用する手法
# minres (ミンレス法)
# ml　（最尤法）
# principal（主因子法）

# rotation 回転法
# varimax (バリマックス回転) 直交法
# promax (プロマックス回転) 斜交法
# oblique (斜め回転)

# impute 欠損値をどうするか
# drop: 削除

# データにフィットさせる
# 因子分析の対象にするのは5観測変数であり，都市名と太平洋側に日本海側ダミー変数は使わない
fa_model.fit(df_sea_side_city.iloc[:, 2:])

# 因子負荷量はloadings_プロパティで読み出せるので，結果のDataFrameを作る
# 因子負荷量：因子と観測変数の間の関係性の強弱のこと

# わかりやすく列名を，元のデータフレームから持ってきて挿入する
# 0列目はラベルなので，1列目から
columns_name_array = df_sea_side_city.columns[2:]
# 行名(index)として，この配列を用いて，DataFrameを作る
df_result = pd.DataFrame(fa_model.loadings_, index=columns_name_array)

# 因子負荷量の行列を色分けして表示
cm = sns.light_palette('red', as_cmap=True
# セルの最後に実行すること．df.head()と同じく，printしても色分けされない
df_result.style.background_gradient(cmap=cm)

5つ目のセルの結果は以下の通り．

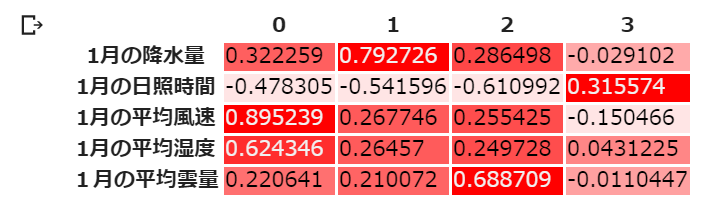
Varimax回転をPromax回転に変えるなどして，回転方法によって結果が変わることを確かめる．（ただしPromax回転の場合因子負荷量に意味はないので参考程度に）

因子分析が「うまくいった」と判断される因子負荷量は「1観測変数に対して，1共通因子だけ1もしくは-1に近く，他の共通因子では0に近い」である．逆に．1つの観測変数に対して因子負荷量の共通因子間の差が小さい場合は因子分析がうまくいかなかったことを示している．

この共通因子数4を仮定した例では，日照時間に関して，負の方向では因子間の違いがあまりない（共通因子2と4の間がほとんど差がない）ことから，因子分析がうまくいっておらず，共通因子数4を仮定するのは，あまり具合が良くない，と言うことがわかる．

6つ目のセル．Varimax回転を使っている場合，累積寄与率を出すことができる．寄与率は主成分分析の時と同じく，「設定した因子で観測データをどのぐらい説明できるか」の基準である．6つ目のセルではこの累積を算出する．

# Varimax回転の場合の因子数4での累積寄与率
factor_index = list([])
for i in range(n_factors):
  factor_index.append('因子' + str(i))
df_cumulative_variance = pd.DataFrame(fa_model.get_factor_variance()[2], index=factor_index)
df_cumulative_variance.style.background_gradient(cmap=cm)

6つ目のセルの出力結果は以下の通り

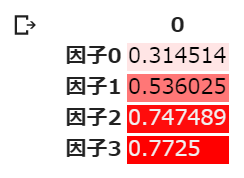
Varimax回転の場合は，累積寄与率を参照することができる．（Promax回転場合は，累積寄与率は出ても値に意味はない．寄与率そのものは相対的に扱うことができる）

3因子で全体の74.7%，４因子で全体の77.2%を「説明することができている」

因子3の寄与率が高くないので，やはり因子数が4の設定では多すぎる，と判断することができる．

7つ目のセルでは因子数4の時の，観測値を共通因子に変換し，その散布図を描く．共通因子数4次元なのでそれぞれの因子を軸にとると，3*2で6つのグラフを描くことができる．

# 因子分析の結果を使って，
# 観測された元々の説明変数の値を潜在変数の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df_sea_side_city.iloc[:, 2:]))
num_of_row = df_sea_side_city.values.shape[0]

# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
kamaishi = list([])
for i in range(num_of_row):
  if df_sea_side_city.values[i][0] == 'Akita':
    akita.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Miyako':
    miyako.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Sakata':
    sakata.append(factors_df.iloc[i, :])
  else:
    kamaishi.append(factors_df.iloc[i, :])

df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_kamaishi = pd.DataFrame(kamaishi)

import matplotlib.pyplot as plt

plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 0], df_kamaishi.iloc[:, 1], label='Kamaishi')

plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()

plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 2], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 2], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 2], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 0], df_kamaishi.iloc[:, 2], label='Kamaishi')

plt.xlabel('Factor0')
plt.ylabel('Factor2')
plt.legend()
plt.show()

plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 0], df_kamaishi.iloc[:, 3], label='Kamaishi')

plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()

plt.scatter(df_akita.iloc[:, 1], df_akita.iloc[:, 2], label='Akita')
plt.scatter(df_sakata.iloc[:, 1], df_sakata.iloc[:, 2], label='Sakata')
plt.scatter(df_miyako.iloc[:, 1], df_miyako.iloc[:, 2], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 1], df_kamaishi.iloc[:, 2], label='Kamaishi')

plt.xlabel('Factor1')
plt.ylabel('Factor2')
plt.legend()
plt.show()

plt.scatter(df_akita.iloc[:, 1], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 1], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 1], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 1], df_kamaishi.iloc[:, 3], label='Kamaishi')

plt.xlabel('Factor1')
plt.ylabel('Factor3')
plt.legend()
plt.show()

plt.scatter(df_akita.iloc[:, 2], df_akita.iloc[:, 3], label='Akita')
plt.scatter(df_sakata.iloc[:, 2], df_sakata.iloc[:, 3], label='Sakata')
plt.scatter(df_miyako.iloc[:, 2], df_miyako.iloc[:, 3], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 2], df_kamaishi.iloc[:, 3], label='Kamaishi')

plt.xlabel('Factor2')
plt.ylabel('Factor3')
plt.legend()
plt.show()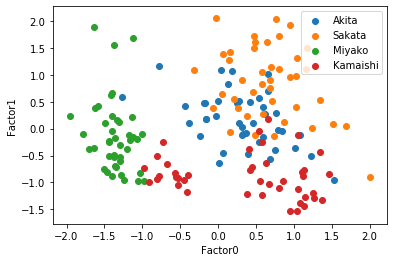

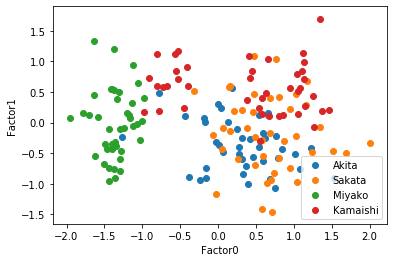
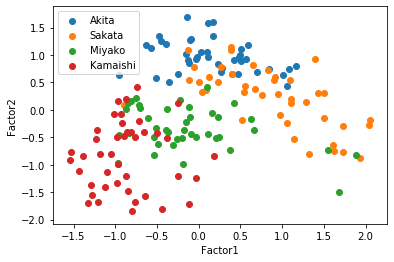
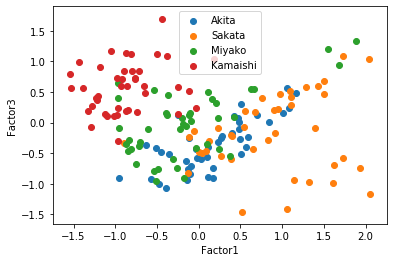
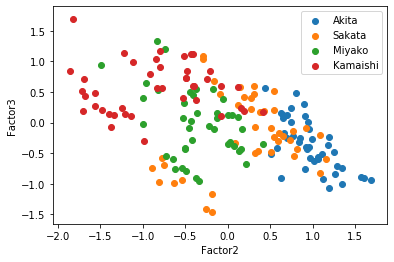
この散布図を見ると，因子1-2の散布図，因子1-3の両方で太平洋側と日本海側を直線で分けられるように見える，因子負荷量を考えると，もっと因子数が少ない方がいいかもしれない．そこで因子数3と2についてもまったく同じように行っていく．

8つ目のセル．因子数3に設定して，まったく同じように因子分析を行い，因子負荷量を出す．

# 因子数3
n_factors=3

fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
fa_model.fit(df_sea_side_city.iloc[:, 2:])

# わかりやすく列名を，元のデータフレームから持ってきて挿入する
# 0列目はラベルなので，1列目から
columns_name_array = df_sea_side_city.columns[2:]
# 行名(index)として，この配列を用いて，DataFrameを作る
df_result = pd.DataFrame(fa_model.loadings_, index=columns_name_array)

# 因子負荷量の行列を色分けして表示
cm = sns.light_palette('red', as_cmap=True)
# セルの最後に実行すること．df.head()と同じく，printしても色分けされない
df_result.style.background_gradient(cmap=cm)

8つ目のセルの結果は以下の通り．

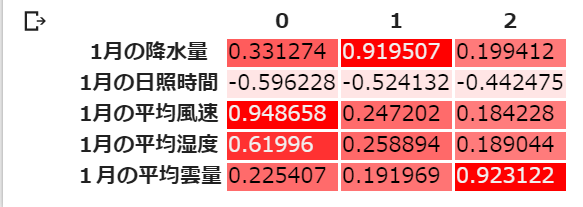
日照時間の因子負荷量の因子間の違いが，因子0と因子1間で0.07, 因子1と因子2間で0.08と，非常に小さい．これは因子数3では因子分析がうまくいかなかったことを示している．

9つ目のセルでは，一応累積寄与率も出してみる．（前述のようにVarimax回転の時に有効．Promax回転の時は無効）

# Varimax回転の時の因子数3での累積寄与率
# Varimax回転の場合は，累積寄与率を参照することができる．
factor_index = list([])
for i in range(n_factors):
  factor_index.append('因子' + str(i))
df_cumulative_variance = pd.DataFrame(fa_model.get_factor_variance()[2], index=factor_index)
df_cumulative_variance.style.background_gradient(cmap=cm)

9つ目のセルの実行結果は以下の通り．

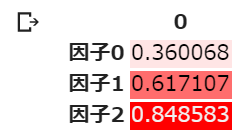
3因子の累積寄与率が84.9%なので，因子数3で因子分析を行った方が全体をうまく説明できていることになるが，因子負荷量の差が小さいことを考えると，総合的にはよくない．

10個目のセルは因子数2に設定して，まったく同じように，因子分析を行い，因子負荷量を出している．

# 因子数2
n_factors=2

fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='varimax', impute='drop')
fa_model.fit(df_sea_side_city.iloc[:, 2:])

# わかりやすく列名を，元のデータフレームから持ってきて挿入する
# 0列目はラベルなので，1列目から
columns_name_array = df_sea_side_city.columns[2:]
# 行名(index)として，この配列を用いて，DataFrameを作る
df_result = pd.DataFrame(fa_model.loadings_, index=columns_name_array)

# 因子負荷量の行列を色分けして表示
cm = sns.light_palette('red', as_cmap=True)
# セルの最後に実行すること．df.head()と同じく，printしても色分けされない
df_result.style.background_gradient(cmap=cm)

10個目のセルの実行結果は以下の通り．

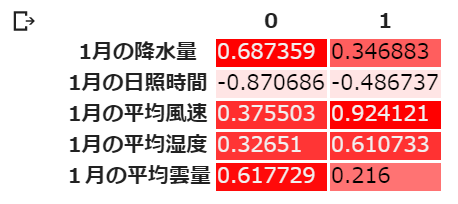
因子数2の時，因子負荷量が因子間でそれなりに大きく離れている．降水量，日照時間，雲量は因子0に，風速と湿度は因子1にそれぞれ大きな影響を受けている．

因子数を3以下にする場合因子数2が適切っぽい．確かめるために散布図を描いてみる．

11個目のセルでは因子数2の時の散布図を描く．因子数2なので2次元グラフ1つ．

# 因子分析の結果を使って，
# 観測された元々の説明変数の値を潜在変数の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df_sea_side_city.iloc[:, 2:]))
num_of_row = df_sea_side_city.values.shape[0]

# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
kamaishi = list([])
for i in range(num_of_row):
  if df_sea_side_city.values[i][0] == 'Akita':
    akita.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Miyako':
    miyako.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Sakata':
    sakata.append(factors_df.iloc[i, :])
  else:
    kamaishi.append(factors_df.iloc[i, :])

df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_kamaishi = pd.DataFrame(kamaishi)

import matplotlib.pyplot as plt

plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 0], df_kamaishi.iloc[:, 1], label='Kamaishi')

plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
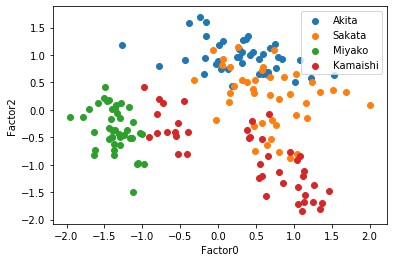
plt.show()

11個目のセルの実行結果は以下の通り．

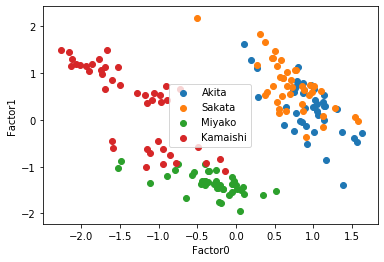
因子数2だと日本海側と太平洋側で直線分離できるので，とりあえずこれで因子に名前を付けることにする．

因子1は平均風速と湿度に正の大きな影響与えている．かつ風速の方が影響が大きい．これは「荒天度」ということができるだろう．

では「降水量」「日照時間」「雲量」に影響を大きく与えている因子0にはどのような名前をつければよいだろうか．日照時間は負の影響であることに注目して名前を付けてみよう．

12個目のセルは以下の通りである．因子数2の時の「共通性」，つまり各観測変数がどれだけ共通因子に影響を受けているかを出す．

# 共通性
# 共通性とは，観測可能な変数における共通因子が占める割合のこと．
# これが低くなると独自因子の割合が多くなる．
# つまり共通因子とどれだけ連動しているかの値を見ることができる
df_communalities = pd.DataFrame(fa_model.get_communalities(), index=columns_name_array)
df_communalities.style.background_gradient(cmap=cm)

12個目のセルの実行結果は以下の通り．

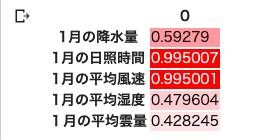
日照時間と風速の値が大きいので，日照時間は因子0の影響を降水量や雲量よりも大きく受けている，風速は因子1の影響を湿度よりも大きく受けている，と言うことができる．

逆に，降水量や雲量，湿度は，日照時間や風速に比べ「共通因子よりも，固有の独自因子の影響を多く受けている」と言うこともできる．

この共通性が非常に小さい時，その観測変数は共通因子から受ける影響が非常に少ないということであり，この観測変数を外して再度因子分析をかけるのが適切である．

「1 - 共通性」の値が「独自性」であり，その変数が共通因子から受けている影響の小ささを表す．

13個目のセルでは，因子数2として，Promax回転の因子分析を行う．

Promax回転（斜交回転）は「因子間に相関性がある」ことを前提とした手法であり，「因子間に相関性がないなんてことは，状況的に考えてそうはない」場合にはこちらを用いる．

# 因子数2のプロマックス回転
n_factors=2

fa_model = FactorAnalyzer(n_factors=n_factors, method='ml', rotation='promax', impute='drop')
fa_model.fit(df_sea_side_city.iloc[:, 2:])

columns_name_array = df_sea_side_city.columns[2:]
df_result = pd.DataFrame(fa_model.loadings_, index=columns_name_array)

cm = sns.light_palette('red', as_cmap=True)
df_result.style.background_gradient(cmap=cm)

13個目のセルの実行結果は以下の通り．プロマックス回転では因子負荷量行列ではなく「パターン行列」と呼ぶ．

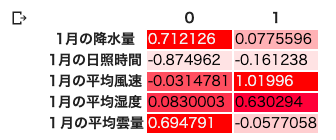
14個目のセルでは，バリマックス回転と全く同じように，潜在変数の散布図を描いた．

# 因子分析の結果を使って，
# 観測された元々の説明変数の値を潜在変数の値に変換する
factors_df = pd.DataFrame(fa_model.transform(df_sea_side_city.iloc[:, 2:]))
num_of_row = df_sea_side_city.values.shape[0]

# 潜在変数の値をプロットしてみる
akita = list([])
miyako = list([])
sakata = list([])
kamaishi = list([])
for i in range(num_of_row):
  if df_sea_side_city.values[i][0] == 'Akita':
    akita.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Miyako':
    miyako.append(factors_df.iloc[i, :])
  elif df_sea_side_city.values[i][0] == 'Sakata':
    sakata.append(factors_df.iloc[i, :])
  else:
    kamaishi.append(factors_df.iloc[i, :])

df_akita = pd.DataFrame(akita)
df_miyako = pd.DataFrame(miyako)
df_sakata = pd.DataFrame(sakata)
df_kamaishi = pd.DataFrame(kamaishi)

import matplotlib.pyplot as plt

plt.scatter(df_akita.iloc[:, 0], df_akita.iloc[:, 1], label='Akita')
plt.scatter(df_sakata.iloc[:, 0], df_sakata.iloc[:, 1], label='Sakata')
plt.scatter(df_miyako.iloc[:, 0], df_miyako.iloc[:, 1], label='Miyako')
plt.scatter(df_kamaishi.iloc[:, 0], df_kamaishi.iloc[:, 1], label='Kamaishi')

plt.xlabel('Factor0')
plt.ylabel('Factor1')
plt.legend()
plt.show()

14個目のセルの実行結果は以下の通り．斜交回転だと軸に沿って出力されるのがわかる．

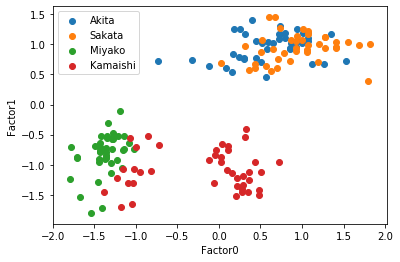
プロマックス回転だと，日本海側と太平洋側がはっきり分離する．したがってこの場合「因子1は太平洋側と日本海側」だと考えることができそうだ．

また，日本海側の都市はPromax回転でも分離して見えないが，宮古と釜石は分離して見えるようになる．因子0が宮古と釜石の違いであると言えそうだ．さて因子0はなんと名前をつければいいだろうか．考えてみよう．

今回も「気温以外のデータ」を使って，さらに線形二項分類の時よりも観測データを多くして，太平洋側の都市と日本海側の都市を比較してみる．

因子分析

因子分析とは，観測された変数の「原因となっている何らかの変数」が隠れて存在する（潜在変数）と考え，その変数を探す分析のことである．

例えば太平洋側の都市と日本海側の都市では冬の気候に大きな違いがあるが，観測データには何らかの「観測可能なデータの違い」があり，その観測可能なデータから「原因」である「気候の違い」を，「なるべく少ない要素」で表現できるように探すことが目的である．

「どちらか側の海」というのは根本的な原因であるダミー変数だが，ダミー変数を直接出せるほど因子分析は優れてはいないので，潜在変数はスカラ値であることがほとんどである．

次元圧縮としても使えてしまうため，主成分分析と混同されることがあるが，因子分析と主成分分析は考え方が逆である．

因子分析は「観測可能なデータから，観測データの原因となっている少数の要素（因子，潜在変数）があると仮定して，それを推測する」

主成分分析は「観測可能なデータから，少数で多くの観測データを上手く表現することができる少数の合成変数を作成する」

である．

実際には「共通因子」に，どのぐらい共通因子が占める割合が大きいかの「因子負荷量」を掛け，その変数の独自の要素である「独自因子」を足したものが，観測データである．

因子分析の特徴として，因子の数がいくつあるかを与えなければならない．因子分析の手法は多く提唱されており色々な組み合わせがあるが，「回転法」が直交法 - Varimax回転の時に因子数の指標となるのが「因子負荷量」である．

因子負荷量は，その仮定した因子がどのぐらい各観測変数に影響を与えているか（正確には各観測変数と各因子の相関係数，つまり連動して動いているか）を見るもので，因子負荷量が各変数において各因子間の違いが大きければ大きいほど，その仮定した因子数は適切である，と考える．（相関係数なので-1から1の間に収まる．0の時は「観測変数とその因子は全く連動していない」ということになる．）

具体的には，「各変数の各因子に対する因子負荷量を見て，一つの因子のみ1（もしくは-1）に近く，他の因子は0に近い」場合には，その因子の選定は適切である，となる．

データの取得と加工

例によって，気象庁オープンデータのページから，

都市は，秋田県→秋田市，岩手県→宮古市，山形県→酒田市，宮城県→石巻市，の順で，それぞれ選択．

今回も「気温以外のデータ」なので，気温は選択しない．

月別の値を選択し，降水量の月合計，

日照時間の月合計，

月平均風速，

湿度/気圧の月平均蒸気圧，を選択し，

平均雲量，を選択し，

1977年〜2018年の「1月」のデータをダウンロードする．

表示オプションはデフォルト．地点の順番と，項目の順番を確認すること．

実際のCSVファイルは，この通りである．

Googleスプレッドシートに読み込む．スタック形式のデータにする．

いつものように不要な行と列を削除．年月の列も使わないので削除．

一番左の列を選択肢，右クリック→「1列左に挿入」で，「観測地点」を記入する列を挿入

作られた列の冒頭に「観測地点」の列名を記入．

観測地点列に「秋田」を入力．

宮古の観測データを洗濯して，右クリック→「切り取り」

秋田の下に貼り付ける．一番左は「観測地点」列なので，列を間違わないこと．

観測地点列に「宮古」を入力．

同じく酒田のデータを作成．

同じく石巻のデータを作成．

列名を短く整える．

これまでと同じ様に，ファイル→ウェブに公開．

CSV形式でウェブに公開してURLをコピーしておく．

いつものようにRに読み込んで，最初の数行を表示する．

url <- '公開したURL'
df <- read.csv(url, header=TRUE)
head(df)

欠損データ行の削除

データ加工の途中でわかったと思うが「平均雲量」は欠損が大きい．（おそらく気象庁内で観測基準が変わったため？）欠損している行を削除する必要がある．

t検定の項でもやったが，欠損地がある行を丸ごと削除するのは以下のプログラムである．

# 欠損値のある行を削除して，df変数に再代入
df <- na.omit(df)

psychパッケージの中の因子分析関数fa

Rの標準の因子分析パッケージは，共通因子が2で固定など，ほぼ役に立たないので，psychパッケージの中に入っているfa間数を使う．

# ライブラリを使う宣言
library("psych")
library("GPArotation") # こっちは回転に使うライブラリ

共通因子数の決定

因子分析は，最初に「幾つの共通因子があるか」を与えなければならない．共通因子数を変えながら探索的に共通因子数を探ることを「探索的因子分析」と呼ぶのだが，psychパッケージの中には，この共通因子数を提案してくれるfa.parallelという関数が存在する．

# 因子分析に食わせるのは，観測値なので，観測地点はいらない
df.X <- df[, c('降水量の合計', '日照時間', '平均風速', '平均湿度', '平均雲量')]
fa.parallel(df.X)

結果は以下のようになる．

Parallel analysis suggests that the number of factors =  1  and the number of components =  1 

共通因子数1で説明できると提案されてしまった．

つまり，何か1つの共通する要素だけで，観測値が説明できるんでは？ということになる．

1だと2次元散布図に描きづらいので，共通因子数1の場合と2の場合で実行してみよう．<

psychパッケージのfa関数による因子分析の実行 varimax回転

まず共通因子数1の場合，

result.fa <-fa(r=df.X, nfactors=1, fm="ml", rotate="varimax")
print(result.fa, digits=3, sort=TRUE) #digitsオプションは小数点以下の桁数，sortオプションは表示順が並べ替えられる．

r=オプションはデータを与える．nfactors=共通因子数オプションで，共通因子数を与える．fm=オプションは算出法であり，とりあえず今回は一般的な最尤法であるmlを指定しておく．rotation=オプションは回転方法を与える．varimax法を与えておく．

結果は以下のようになる．

Factor Analysis using method =  ml
Call: fa(r = df.X, nfactors = 1, rotate = "varimax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
             V    ML1    h2      u2 com
平均雲量     5  0.998 0.995 0.00498   1
日照時間     2 -0.976 0.953 0.04741   1
平均風速     3  0.853 0.727 0.27305   1
降水量の合計 1  0.717 0.515 0.48520   1
平均湿度     4  0.713 0.508 0.49165   1

                 ML1
SS loadings    3.698
Proportion Var 0.740

Mean item complexity =  1
Test of the hypothesis that 1 factor is sufficient.

The degrees of freedom for the null model are  10  and the objective function was  5.972 with Chi Square of  773.424
The degrees of freedom for the model are 5  and the objective function was  0.306 

The root mean square of the residuals (RMSR) is  0.026 
The df corrected root mean square of the residuals is  0.037 

The harmonic number of observations is  133 with the empirical chi square  1.849  with prob <  0.87 
The total number of observations was  133  with Likelihood Chi Square =  39.442  with prob <  1.93e-07 

Tucker Lewis Index of factoring reliability =  0.9093
RMSEA index =  0.2316  and the 90 % confidence intervals are  0.1654 0.2972
BIC =  14.99
Fit based upon off diagonal values = 0.999
Measures of factor score adequacy             
                                                    ML1
Correlation of (regression) scores with factors   0.998
Multiple R square of scores with factors          0.996
Minimum correlation of possible factor scores     0.991

同じように共通因子数2の因子分析を実行する．

result.fa <- fa(r=df.X, nfactors=2, fm="ml", rotate="varimax")
print(result.fa, digits=3, sort=TRUE)

結果は以下のようになる．

Factor Analysis using method =  ml
Call: fa(r = df.X, nfactors = 2, rotate = "varimax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
             item    ML1    ML2    h2      u2  com
日照時間        2 -0.927 -0.368 0.995 0.00497 1.31
平均雲量        5  0.848  0.509 0.978 0.02187 1.64
平均風速        3  0.711  0.485 0.740 0.26015 1.76
降水量の合計    1  0.679  0.286 0.543 0.45739 1.34
平均湿度        4  0.364  0.803 0.778 0.22222 1.39

                        ML1   ML2
SS loadings           2.677 1.356
Proportion Var        0.535 0.271
Cumulative Var        0.535 0.807
Proportion Explained  0.664 0.336
Cumulative Proportion 0.664 1.000

Mean item complexity =  1.5
Test of the hypothesis that 2 factors are sufficient.

The degrees of freedom for the null model are  10  and the objective function was  5.972 with Chi Square of  773.424
The degrees of freedom for the model are 1  and the objective function was  0.02 

The root mean square of the residuals (RMSR) is  0.011 
The df corrected root mean square of the residuals is  0.033 

The harmonic number of observations is  133 with the empirical chi square  0.293  with prob <  0.588 
The total number of observations was  133  with Likelihood Chi Square =  2.549  with prob <  0.11 

Tucker Lewis Index of factoring reliability =  0.9795
RMSEA index =  0.111  and the 90 % confidence intervals are  0 0.2821
BIC =  -2.341
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                    ML1   ML2
Correlation of (regression) scores with factors   0.975 0.877
Multiple R square of scores with factors          0.951 0.768
Minimum correlation of possible factor scores     0.903 0.537

因子負荷量

それぞれの結果の最初の表のML1が1番目の共通因子の「因子負荷量」（以下ML2も同じ），h2列が「共通性」，u2は「独自性」．

前述の因子分析が想定するモデルで「「共通因子」に「独自因子」を足したものが観測変数として現れている」という説明を図でしたが，この「共通因子」に依存している割合が「共通性」であり，その逆「1-共通性」が「独自性」である．

重量なのが，各共通因子と各観測変数の間の「因子負荷量」である．因子負荷量は「その因子が変数つまり観測された値にどれだけ影響を与えているか」の値で，-1から1の間を取る．

因子分析が「うまくいった」と判断される因子負荷量は「1観測変数に対して，1共通因子だけ1もしくは-1に近く，他の共通因子では0に近い」である．逆に．1つの観測変数に対して因子負荷量の共通因子間の差が小さい場合は因子分析がうまくいかなかったことを示している．

共通因子数2を与えた例では，日照時間に関して，負の方向では因子間の違いがあまりない（共通因子2と4の間がほとんど差がない）ことから，因子分析がうまくいっておらず，共通因子数4を仮定するのは，あまり具合が良くない，と言うことがわかる．

因子寄与率，累積寄与率

2番目の表の「Proportion Var」と「Cumulative Var」はそれぞれ因子寄与率と累積寄与率である．これはVarimax回転の時に有効である．主成分分析の寄与率，累積寄与率とほぼ同じ意味で，共通因子がどれだけデータを説明できているかを表す．（Promax回転場合は，累積寄与率は出ても値に意味はない．寄与率そのものは相対的に扱うことができる）

ちなみにその後の「Proportion Explainded」は「説明率」，「Cumulative Proportion」は「累積説明率」で，合計が1であることから，この場合は寄与率よりもこちらの累積説明率の方が主成分分析に近いイメージ．

Promax回転

今度は共通因子数1と2にそれぞれ，Promax回転を試してみる．

result.fa <-fa(r=df.X, nfactors=1, fm="ml", rotate="promax")
print(result.fa, digits=3, sort=TRUE) 

Factor Analysis using method =  ml
Call: fa(r = df.X, nfactors = 1, rotate = "promax", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
             V    ML1    h2      u2 com
平均雲量     5  0.998 0.995 0.00498   1
日照時間     2 -0.976 0.953 0.04741   1
平均風速     3  0.853 0.727 0.27305   1
降水量の合計 1  0.717 0.515 0.48520   1
平均湿度     4  0.713 0.508 0.49165   1

                 ML1
SS loadings    3.698
Proportion Var 0.740

Mean item complexity =  1
Test of the hypothesis that 1 factor is sufficient.

The degrees of freedom for the null model are  10  and the objective function was  5.972 with Chi Square of  773.424
The degrees of freedom for the model are 5  and the objective function was  0.306 

The root mean square of the residuals (RMSR) is  0.026 
The df corrected root mean square of the residuals is  0.037 

The harmonic number of observations is  133 with the empirical chi square  1.849  with prob <  0.87 
The total number of observations was  133  with Likelihood Chi Square =  39.442  with prob <  1.93e-07 

Tucker Lewis Index of factoring reliability =  0.9093
RMSEA index =  0.2316  and the 90 % confidence intervals are  0.1654 0.2972
BIC =  14.99
Fit based upon off diagonal values = 0.999
Measures of factor score adequacy             
                                                    ML1
Correlation of (regression) scores with factors   0.998
Multiple R square of scores with factors          0.996
Minimum correlation of possible factor scores     0.991

Factor Analysis using method =  ml
Call: fa(r = df.X, nfactors = 2, rotate = "promax", fm = "ml")

 Warning: A Heywood case was detected. 
Standardized loadings (pattern matrix) based upon correlation matrix
             item    ML1    ML2    h2      u2  com
日照時間        2 -1.041  0.059 0.995 0.00497 1.01
平均雲量        5  0.847  0.181 0.978 0.02187 1.09
降水量の合計    1  0.752 -0.021 0.543 0.45739 1.00
平均風速        3  0.673  0.232 0.740 0.26015 1.23
平均湿度        4  0.003  0.880 0.778 0.22222 1.00

                        ML1   ML2
SS loadings           2.994 1.039
Proportion Var        0.599 0.208
Cumulative Var        0.599 0.807
Proportion Explained  0.742 0.258
Cumulative Proportion 0.742 1.000

 With factor correlations of 
      ML1   ML2
ML1 1.000 0.745
ML2 0.745 1.000

Mean item complexity =  1.1
Test of the hypothesis that 2 factors are sufficient.

The degrees of freedom for the null model are  10  and the objective function was  5.972 with Chi Square of  773.424
The degrees of freedom for the model are 1  and the objective function was  0.02 

The root mean square of the residuals (RMSR) is  0.011 
The df corrected root mean square of the residuals is  0.033 

The harmonic number of observations is  133 with the empirical chi square  0.293  with prob <  0.588 
The total number of observations was  133  with Likelihood Chi Square =  2.549  with prob <  0.11 

Tucker Lewis Index of factoring reliability =  0.9795
RMSEA index =  0.111  and the 90 % confidence intervals are  0 0.2821
BIC =  -2.341
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                    ML1   ML2
Correlation of (regression) scores with factors   0.998 0.935
Multiple R square of scores with factors          0.996 0.875
Minimum correlation of possible factor scores     0.992 0.749

共通因子数2の結果を見ると，共通因子1（ML1）と共通因子2（ML2）の因子負荷量の差が，varimax回転の時に比べ非常に大きい．つまり因子分析が成功したと考えられる．

varimax回転はごく基本的な処理で（直交回転と呼ぶ），Promax回転（斜交回転）の方が性能がいいようだ．

結果の解釈

因子分析で一番重要となのは結果の解釈である．わかりやすいので，Promax回転の共通因子数2の場合を見てみよう．結果を再掲する．

             item    ML1    ML2    h2      u2  com
日照時間        2 -1.041  0.059 0.995 0.00497 1.01
平均雲量        5  0.847  0.181 0.978 0.02187 1.09
降水量の合計    1  0.752 -0.021 0.543 0.45739 1.00
平均風速        3  0.673  0.232 0.740 0.26015 1.23
平均湿度        4  0.003  0.880 0.778 0.22222 1.00

共通因子1（ML1）は，日照時間の因子負荷量が1or-1に近く，かつ共通性が非常に高いことから，日照時間に強く影響を与えている．同じように（日照時間ほどではないが）平均雲量と降水量の合計，平均風速に大きく影響を与えている．

ここで「1月のデータ」だったことを思い出そう．太平洋側と日本海側の都市の冬の気候は，日本海側が基本的に荒天であり，太平洋側は基本的に晴天である．日本海側は冬の日照時間がほとんどなく（日照時間が0からほぼ動かない，つまり負の影響が出る，また，雲の量が多い），かつ雪が降る（降水量はプラスの方向に動く，つまり正の方向に影響が出る）と考えると，共通因子1（ML1）は明確に，「太平洋側の都市かどうか」を表していると言えるのではないだろうか．

つまり，この共通因子1は，前回の二項分類で使った太平洋側日本海側ダミー変数そのものということができる．

風速は，日照時間ほどではないが，同じく影響を太平洋側日本海側に大きく与えている．

平均湿度に関してはどうだろう？　共通因子1つまり太平洋側か日本海側かにはほぼ影響を受けていないことがわかる．平均湿度に影響を与えている共通因子2はどうやら別の要素らしい．元データを見返しながら，観測値の4都市の気候を分析し，この共通因子2に名前をつけてみよう．

今回は，「気温以外のデータ」を使って，太平洋側の都市と日本海側の都市の分類器を作成してみる．

線形二項分類

線形分類(Linear Classification)とは，2つのカテゴリが入っているデータの集合の真ん中に一本直線を引くことで，カテゴリ分けする境目を定め，予測したいデータが入ってきた時に，どちらかに分類する問題である．もちろん人間が一本線を引くことで行うこともできるが，これを機械学習で行う．

入力するデータが2次元，例えば「降水量，日照時間」だった場合には，カテゴリ分けする境目は「直線」になるが，「降水量，日照時間，湿度」のように3次元になると「2次元平面」になり，「降水量，日照時間，湿度，風速」のように4次元だと「3次元超平面」になる．

3次元空間上の平面ぐらいは平面に表示するグラフでなんとか表示できるものの，4次元以上は無理なので，写像をするか「4次元の線形の式」として理解するしかない．

本項では，線形Support Vector Machine(Linear SVM)と，ロジスティック回帰(Logistic Regression）による，分類器というか，つまり直線に必要な「係数」および「切片」を学習する．

ロジスティック回帰は「回帰」と名がついているが，分類問題に使う．分ける直線を学習するので「線形回帰」とも言えるので，この名前がついている．

ダミー変数とカテゴリ変数

日本海側と太平洋側の年を分類すると書いたが，SVMやロジスティック回帰で機械学習するためには，これを数字に直さなければならない．もちろん太平洋側と日本海側は大小の比較ができないなど「値」としては，意味がないわけで，ここでは太平洋側を0，日本海側を1として表すことにする．

このように，その要素の有無で0と1の2値で表現される変数，その大小や差に意味がないものを「ダミー変数」と呼ぶ．(回帰分析でもダミー変数を使うことができる．)

例えば北海道の都市のように「太平洋側，日本海側，オホーツク海側」のように3つ以上の状態があり，2値で表すことができないもの，つまり「0, 1, 2, 3...などの状態が複数あり，かつその数字が大小の意味を持ってない場合」は，カテゴリ変数と呼ぶ

カテゴリ変数は二項分類つまりここでおこなような「AとBのどっち？」の問題では扱えないので，カテゴリ変数で表現している内容を，要素に分けて，要素の有無で表現，つまり複数のダミー変数に直すなどの方法をとる．

データの取得と加工

例によって，気象庁オープンデータのページから，

都市は，秋田県→秋田市，岩手県→宮古市，山形県→酒田市，宮城県→石巻市，新潟県→新潟市，茨城県→水戸市，千葉県→銚子市，の順で，それぞれ選択．

月別の値を選択し，降水量の月合計，

日照時間の月合計，

月平均風速，

湿度/気圧の月平均蒸気圧，を選択し，

1977年〜2018年の「1月」のデータをダウンロードする．

表示オプションはデフォルト．地点の順番と，項目の順番を確認すること．

ダウンロードしたCSVはこんな見た目になる．

実際のCSVファイルは，この通りである．

このCSVを「太平洋側日本海側ダミー変数」を加えたスタック形式のデータに加工する．

Google Spreadsheetに上記CSVを読み込んだ状態．

例によって不要な行と列を削除する．降水量に関しては「現象なし情報」という列も含まれているので注意．

秋田, 宮古, 酒田, 石巻, 新潟, 水戸, 銚子を抽出するために新しいスプレッドシートのワークブックを作る．

ワークブック名とシート名を整える

変数名・列名を入れる．観測地点，太平洋側日本海側ダミー，降水量の合計，日照時間，平均風速，平均蒸気圧．

太平洋側日本海側ダミー変数は，太平洋側を0，日本海側を1と決めておく．

元のワークブックから，秋田の1977年〜2018年のデータを選択して，右クリック→コピー．

新しいワークブックの方の降水量のセルを指定して，右クリック→貼り付け．列の場所を間違えないように．

貼り付けられた状態．

観測地点列の頭に「秋田」を記入し，コピー．

その下，41行（残り41年分）の行の観測地点の列を選択して，貼り付け．

太平洋側日本海側ダミーの列に「1」を記入．前述のように太平洋側の都市が0で，日本海側の都市が1，秋田は「1」．コピー．

その下，41行（残り41年分）の行の太平洋側日本海側ダミーの列を選択して，貼り付け．

貼り付けられた状態．

同じように宮古（太平洋側），

酒田（日本海側），

石巻（太平洋側），

新潟（日本海側），

水戸（太平洋側），

銚子（太平洋側）のデータを作成する．

いつもと同じように，新しい方のワークブックのシートをファイル→ウェブに公開．

シートを，CSVとして公開する

Google Colabに読み込んで，pd.DataFrameとして読み込み最初の数行を表示．

目的変数Y（太平洋側日本海側ダミー）と，説明変数X（観測値）のnumpy配列に分けておく．

# 目的変数Yは「太平洋側か日本海側か」つまり，ダミー変数の列になる
y_whole = df.loc[:, '太平洋側日本海側ダミー']
# npの1次元配列に変換
y_whole = np.ravel(y_whole)

x_whole = df.loc[:, ['降水量の合計', '日照時間', '平均風速', '平均蒸気圧']]
# 目的変数Xは観測値4次元からなる．pd.DataFrameのまま使える．

訓練データとテストデータ

前述の通り，線形二項分類は「データをうまく判別できるような直線を引く」ことで分類を行うが，これは言い換えれば，直線を表す式 y = ax + b のaとbを「機械学習」することである．

機械学習とは，自動的に「学習」の手順を定めて繰り返し行うことで，厳密ではないものの正解に近い解（近似解）に徐々に近づけていくことであるが，その時に訓練データ（トレーニングデータ）とテストデータの2つのデータセットを用いる．

訓練データを使って学習して，訓練データで表現される正解に近づいていくのは当然と言えば当然で，そこで学習の過程で「訓練データを使って学習して，テストデータでどれだけ正解に近いかを判別する」という流れを取る．そのために訓練データとテストデータは別のものにしておく必要がある．

とは言っても実際には「今持っているデータの半分を訓練データとして使い，残り半分をテストデータとして使うように指示する」だけである．スタック形式のデータが1000行分あれば，ランダムに500行抽出して訓練データとし，残り500行をテストデータにする，という形である．これはscikit-learnの中に入っている関数train_test_split関数で簡単にできる．

from sklearn.model_selection import train_test_split
# 関数を実行するだけで，ランダムに訓練データとテストデータを分けてくれる．
x_train, x_test, y_train, y_test = train_test_split(x_whole, y_whole)

線形SVM

Support Vector Machine, SVMは，本来，非線形空間を線形に捻じ曲げて判別するためのものであり，今回のような最初から線形のものに使う意味はあまりないが，ごく基本的な線形分類学習機としても有効である．

scikit-learnで用意されているものは，大体この手順．まずモデルを呼び出しインスタンス化（実行可能な状態にする），fit関数に訓練データを与えて学習し，predict関数にテストデータを与えて，テストデータの方の予測値を出す．予測値と実際の値（ここでは太平洋側か日本海側か）をmetrics.accuracy_score関数に与え，正答率を出す，という流れ．

from sklearn.svm import LinearSVC
from sklearn import metrics

# モデルを呼び出して
svm_model = LinearSVC(C=1.0)
# fit関数に訓練データを入れて学習を実行する
svm_model.fit(x_train, y_train)

# predict関数にテストデータを入れて，学習結果をもとにテストデータを入れたときの「予測値」を計算する
svm_y_predict = svm_model.predict(x_test)

# テストデータの実際の値と予測値から正答率を計算する
svm_accuracy_score = metrics.accuracy_score(y_test, svm_y_predict)
print('svmの正答率', svm_accuracy_score)
# 係数がこの中に入っている．この係数で表される4次元空間の平面で切るとうまく分類できる，という意味
print('分離平面の係数', svm_model.coef_[0])
print('分離平面の切片', svm_model.intercept_[0])

# 分離平面の係数をもうちょっとわかりやすく表示してみる
x_labels = ['降水量の合計', '日照時間', '平均風速', '平均蒸気圧']
svm_coef_df = pd.DataFrame([x_labels, svm_model.coef_[0]]).T
# DataFrame.Tはnumpyのtransposeに相当し，配列の次元を入れ替える
print(svm_coef_df)

結果は以下のようになる．訓練データとテストデータの分離やSVMの学習は，その時ごとに代わるので，必ずしもここまでいい結果が出るとは限らない．（というか，この結果は良すぎる）

svmの正答率 0.8648648648648649
分離平面の係数 [ 0.00037371 -0.01198279  0.3370101  -0.03095341]
分離平面の切片 0.05048275469556343
        0            1
0  降水量の合計  0.000373713
1    日照時間   -0.0119828
2    平均風速      0.33701
3   平均蒸気圧   -0.0309534

正答率は0.86とそこそこ高い．つまり4次元の空間上で，この傾きと切片により，直線（面というか立体というか）を引けば，ほぼ太平洋側と日本海側の都市を分離できる，ということになる．

ではさらに未知の都市，鳥取県境（日本海側）および静岡県石廊崎（太平洋側）の，2018年1月のデータを入れて，ちゃんと判別できるか見てみよう．

# 鳥取県境(日本海側)，静岡県石廊崎(太平洋側)の2018年1月のデータを入れてみて，ちゃんと分類できるか検証する．
# 境のデータ 降水量191.5(mm), 日照時間58.1(時間), 平均風速2.6(m), 平均蒸気圧6.3(hPa), 
# 石廊崎のデータ 降水量 93.5(mm), 日照時間188.6(時間), 平均風速6.8(m), 平均蒸気圧6.6(hPa)
sakaiX = np.array([[191.5, 58.1, 2.6, 6.3]], dtype=np.float)
irouzakiX = np.array([[93.5, 188.6, 6.8, 6.6]], dtype=np.float)

print('境の2018年1月のデータから予測した結果', svm_model.predict(sakaiX))
print('石廊崎の2018年1月のデータから予測した結果', svm_model.predict(irouzakiX))

結果は以下の通り．

境の2018年1月のデータから予測した結果 [1.]
石廊崎の2018年1月のデータから予測した結果 [0.]

6つ目のセルの結果は以下のようになる．境が1，石廊崎が0と判断されているので，学習したSVMの分類はそれなりに正しいようだ．もちろんさらに学習の精度を検証するために，他の都市，他の地点のデータを突っ込んで，確かめてみるのも良い．

ただしこれは「何回か学習を実行してかなり高い正答率になったSVMに突っ込んだ結果」である．実際には正答率の平均はもっと低い．結果を観察してみると，主に「太平洋側の都市を日本海側として間違えて判別する」例は少ないが，「日本海側の都市を太平洋側として間違えて判別する」例が多いようだ．

ロジスティック回帰

まったく同じデータを，ロジスティック回帰で分類の学習をしてみる．ロジスティック回帰は基本的に線形分類問題，つまり今回のように「直線を引くことで分類できる」問題に特化した手法である．

SVMと同じくscikit-learnに含まれているので，手順もSVMの時と全く同じである．モデルを読み込み，訓練データをfitし，テストデータをpredictして，正答率を出す．

from sklearn.linear_model import LogisticRegression
# X, Yの訓練データでロジスティック回帰を学習する
log_model = LogisticRegression()
log_model.fit(x_train, y_train)

# 学習済みのモデルにXテストデータをつっこみ，Yを予測し，観測データと比較
log_y_predict = log_model.predict(x_test)
log_accuracy_score = metrics.accuracy_score(y_test, log_y_predict)
print('ロジスティック回帰の正答率:', log_accuracy_score)
# 係数がこの中に入っている．この係数で表される4次元空間の平面で切るとうまく分類できる，という意味
print('分離平面の係数', log_model.coef_[0])
print('分離平面の切片', log_model.intercept_[0])

# 同じく分離平面の係数をもうちょっとわかりやすく表示してみる
log_coef_df = pd.DataFrame([x_labels, log_model.coef_[0]]).T
print(log_coef_df)

実行結果は以下のようになる．ロジスティック回帰は何度学習を実行しても同じ結果が出る（内部的にニュートン法を使っている）．ただし当然ながら訓練データとテストデータの分割を再度ランダムに行うと，結果は変わる．

ロジスティック回帰の正答率: 0.9682539682539683
分離平面の係数 [-0.00933651 -0.0580769   1.47516013 -1.16708297]
分離平面の切片 4.020109595993421
        0           1
0  降水量の合計 -0.00933651
1    日照時間  -0.0580769
2    平均風速     1.47516
3   平均蒸気圧    -1.16708

SVMの時と同じく，鳥取県境と静岡県石廊崎の2018年1月のデータから，太平洋側か日本海側かを予測させてみよう．

sakaiX = np.array([[191.5, 58.1, 2.6, 6.3]], dtype=np.float)
irouzakiX = np.array([[93.5, 188.6, 6.8, 6.6]], dtype=np.float)

print('境の2018年1月のデータから予測した結果', log_model.predict(sakaiX))
print('石廊崎の2018年1月のデータから予測した結果', log_model.predict(irouzakiX))

結果は以下のようになる．

境の2018年1月のデータから予測した結果 [1.]
石廊崎の2018年1月のデータから予測した結果 [0.]

ちゃんと分類できているが，やはり訓練データとテストデータの分け方によって予測精度にだいぶ差が出る．SVMの時と同じく，「日本海側の都市を誤って太平洋側」と判別している率が高い．

つまり，1月の降水量，1月の日照時間，1月の風速平均，1月の湿度の4つの観測値は，日本海側と太平洋側を判定するのには不十分である，と言える．別の観測値を使って予測精度を上げてみよう．

今回は，「気温以外のデータ」を使って，太平洋側の都市と日本海側の都市の分類器を作成してみる．

線形二項分類

線形分類(Linear Classification)とは，2つのカテゴリが入っているデータの集合の真ん中に一本直線を引くことで，カテゴリ分けする境目を定め，予測したいデータが入ってきた時に，どちらかに分類する問題である．もちろん人間が一本線を引くことで行うこともできるが，これを機械学習で行う．

入力するデータが2次元，例えば「降水量，日照時間」だった場合には，カテゴリ分けする境目は「直線」になるが，「降水量，日照時間，湿度」のように3次元になると「2次元平面」になり，「降水量，日照時間，湿度，風速」のように4次元だと「3次元超平面」になる．

3次元空間上の平面ぐらいは平面に表示するグラフでなんとか表示できるものの，4次元以上は無理なので，写像をするか「4次元の線形の式」として理解するしかない．

本項では，線形Support Vector Machine(Linear SVM)と，ロジスティック回帰(Logistic Regression）による，分類器というか，つまり直線に必要な「係数」および「切片」を学習する．

ロジスティック回帰は「回帰」と名がついているが，分類問題に使う．分ける直線を学習するので「線形回帰」とも言えるので，この名前がついている．

ダミー変数とカテゴリ変数

日本海側と太平洋側の年を分類すると書いたが，SVMやロジスティック回帰で機械学習するためには，これを数字に直さなければならない．もちろん太平洋側と日本海側は大小の比較ができないなど「値」としては，意味がないわけで，ここでは太平洋側を0，日本海側を1として表すことにする．

このように，その要素の有無で0と1の2値で表現される変数，その大小や差に意味がないものを「ダミー変数」と呼ぶ．(回帰分析でもダミー変数を使うことができる．)

例えば北海道の都市のように「太平洋側，日本海側，オホーツク海側」のように3つ以上の状態があり，2値で表すことができないもの，つまり「0, 1, 2, 3...などの状態が複数あり，かつその数字が大小の意味を持ってない場合」は，カテゴリ変数と呼ぶ

カテゴリ変数は二項分類つまりここでおこなような「AとBのどっち？」の問題では扱えないので，カテゴリ変数で表現している内容を，要素に分けて，要素の有無で表現，つまり複数のダミー変数に直すなどの方法をとる．

データの取得と加工

例によって，気象庁オープンデータのページから，

都市は，秋田県→秋田市，岩手県→宮古市，山形県→酒田市，宮城県→石巻市，新潟県→新潟市，茨城県→水戸市，千葉県→銚子市，の順で，それぞれ選択．

月別の値を選択し，降水量の月合計，

日照時間の月合計，

月平均風速，

湿度/気圧の月平均蒸気圧，を選択し，

1977年〜2018年の「1月」のデータをダウンロードする．

表示オプションはデフォルト．地点の順番と，項目の順番を確認すること．

ダウンロードしたCSVはこんな見た目になる．

実際のCSVファイルは，この通りである．

このCSVを「太平洋側日本海側ダミー変数」を加えたスタック形式のデータに加工する．

Google Spreadsheetに上記CSVを読み込んだ状態．

例によって不要な行と列を削除する．降水量に関しては「現象なし情報」という列も含まれているので注意．

秋田, 宮古, 酒田, 石巻, 新潟, 水戸, 銚子を抽出するために新しいスプレッドシートのワークブックを作る．

ワークブック名とシート名を整える

変数名・列名を入れる．観測地点，太平洋側日本海側ダミー，降水量の合計，日照時間，平均風速，平均蒸気圧．

太平洋側日本海側ダミー変数は，太平洋側を0，日本海側を1と決めておく．

元のワークブックから，秋田の1977年〜2018年のデータを選択して，右クリック→コピー．

新しいワークブックの方の降水量のセルを指定して，右クリック→貼り付け．列の場所を間違えないように．

貼り付けられた状態．

観測地点列の頭に「秋田」を記入し，コピー．

その下，41行（残り41年分）の行の観測地点の列を選択して，貼り付け．

太平洋側日本海側ダミーの列に「1」を記入．前述のように太平洋側の都市が0で，日本海側の都市が1，秋田は「1」．コピー．

その下，41行（残り41年分）の行の太平洋側日本海側ダミーの列を選択して，貼り付け．

貼り付けられた状態．

同じように宮古（太平洋側），

酒田（日本海側），

石巻（太平洋側），

新潟（日本海側），

水戸（太平洋側），

銚子（太平洋側）のデータを作成する．

いつもと同じように，新しい方のワークブックのシートをファイル→ウェブに公開．

シートを，CSVとして公開する

いつものようにRに読み込んで，最初の数行を表示する．

url <- '公開したURL'
df <- read.csv(url, header=TRUE)
head(df)

訓練データとテストデータ

前述の通り，線形二項分類は「データをうまく判別できるような直線を引く」ことで分類を行うが，これは言い換えれば，直線を表す式 y = ax + b のaとbを「機械学習」することである．

機械学習とは，自動的に「学習」の手順を定めて繰り返し行うことで，厳密ではないものの正解に近い解（近似解）に徐々に近づけていくことであるが，その時に訓練データ（トレーニングデータ）とテストデータの2つのデータセットを用いる．

訓練データを使って学習して，訓練データで表現される正解に近づいていくのは当然と言えば当然で，そこで学習の過程で「訓練データを使って学習して，テストデータでどれだけ正解に近いかを判別する」という流れを取る．そのために訓練データとテストデータは別のものにしておく必要がある．

とは言っても実際には「今持っているデータの半分を訓練データとして使い，残り半分をテストデータとして使うように指示する」だけである．スタック形式のデータが1000行分あれば，ランダムに500行抽出して訓練データとし，残り500行をテストデータにする，という形である．これはRのdata.frameの機能を使うと簡単に実現できる．

# 行数を取得する
num.of.row <- nrow(df)

# 行数からランダムに行番号を抽出．第2引数に0.5をかけているのは，半分抽出するという意味
random.indexes <- sample(num.of.row, num.of.row*0.5)
print(random.indexes)

# 定規の行番号だけを抽出
training.data <- df[random.indexes, ]

# 「それ以外の行」をテストデータとして抽出 与えるindexesの配列に-をつけてやる
test.data <- df[-random.indexes, ]

# 確認
head(training.data)

# こっちは「以外」なので順番に並んでいる
head(test.data)

出力は以下のようになる．

 [1] 107  97  30 185  36 214  28 225  45 227  98 166   2  57 109 129 197  31
 [19]  67 190  77  13 246  79 251 104  12 212 168 167 207 240 143 159  53  58
 [37]  48 213  82  39 187   9 118 144 216   3  84 252 199 194 127 130 183  74
 [55] 141  90 124 112 234  27  65 161 235  42 249  37 162 181 135  89 153  20
 [73] 120 145 114 232 182  95  76 186 176 193 147  75 119 202  11  32  66 158
 [91]  78 247  71 248 121 128  35 210 241 189 203  17  41  63  50 138  61 101
[109] 102 110 163 223 115 140  87 123 188 175  43  69  85 220 177 179 180 221

線形2項分類の目的変数と説明変数，SVM分類期の学習の実施

Rの標準パッケージの中にはSVMは含まれていないので，まずkernlabという追加パッケージをインストールする．インストールするといっても下のプログラムを実行するという形である．

# 線形2項分類を行う線形SVMのためのパッケージを入れる
install.packages("kernlab")
library(kernlab)

「真ん中に直線を引くので，実はやっていることは回帰分析とは変わらない」と前述したが，「2項分類」なので，目的変数は0か1（kernlabのksvmの場合，実際にはここに文字列の値が入っていても良い），説明変数が観測データとなる．

したがって，formulaに与える式は，太平洋側日本海側ダミー ~ .となる．ただしkernlabのksvmはformula=キーワードをつけずに式を直接第1引数に入れるようになっている．（なぜRの基本から外れた実装になっているのかは不明）

今回はダミー変数が目的変数なので，type="C-svc"を入れておくと，ダミー変数を目的変数とした二項分類になる．またデータを標準化・正規化したいのでscaled=TRUEも入れておく．

その後，一度受け取った変数をそのまま1行に書いて「実行」する．

学習が終わったら，テストデータの説明変数だけを抽出したものを食わせて，太平洋側か日本海側の0か1を予測させる．

# 観測地点は不要なので落とす
training.data.df <- training.data[, c('太平洋側日本海側ダミー','降水量の合計', '日照時間', '平均風速', '平均蒸気圧')]

# 回帰のように，式formulaとdata.frameを与える．
# ただしksvmはformula=キーワードを書かずに，第1引数に直接式を書いてやる．
# 今回のようにダミー変数をyに置きたい場合には，type="C-svc"を選択する．
svm.model <- ksvm(太平洋側日本海側ダミー ~ ., data=training.data.df, type="C-svc")
# ここで変数で受け取ったものを「実行する」という行が必要
svm.model

# predict関数で学習済みのSVMにテストデータの説明変数部分を食わせて，予測を得て，test.result変数で受ける
test.result = predict(svm.model, test.data[, c('降水量の合計', '日照時間', '平均風速', '平均蒸気圧')])

# 実際の正解とtest.result変数の中に入っている予測値をtable関数で比較する
table(test.result, test.data[, '太平洋側日本海側ダミー'])

結果は以下のようになる．

Support Vector Machine object of class "ksvm" 

SV type: C-svc  (classification) 
 parameter : cost C = 1 

Gaussian Radial Basis kernel function. 
 Hyperparameter : sigma =  0.773251281075058 

Number of Support Vectors : 55 

Objective Function Value : -21.9573 
Training error : 0.031746 

           
test.result  0  1
          0 86 10
          1  2 28

結果は最後の表になる．正解は0つまり太平洋側なのに1つまり日本海側と予測された観測値のセットが2つあり，また，正解は1つまり日本海側なのに0つまり太平洋側と予測された観測値のセットが10個ある，ということになる．現状では正解率はあまりよくないようだ．

ksvm関数にオプションで指定する学習パラメータをうまく調整してやると，この学習率が上がることもある．また前項で触れた「標準化・正規化」のような前処理を予めデータに対してかけておくなどの方法も考えられる．

では，さらに未知のデータを食わせてみよう．

# 鳥取県境(日本海側)，静岡県石廊崎(太平洋側)の2018年1月のデータを入れてみて，ちゃんと分類できるか検証する．
# 境のデータ 降水量191.5(mm), 日照時間58.1(時間), 平均風速2.6(m), 平均蒸気圧6.3(hPa), 
# 石廊崎のデータ 降水量 93.5(mm), 日照時間188.6(時間), 平均風速6.8(m), 平均蒸気圧6.6(hPa)
sakai.X <- data.frame('降水量の合計'=c(191.5), '日照時間'=c(58.1), '平均風速'=c(2.6), '平均蒸気圧'=c(6.3))
print(predict(svm.model, sakai.X))

irouzaki.X <- data.frame('降水量の合計'=c(93.5), '日照時間'=c(188.6), '平均風速'=c(6.8), '平均蒸気圧'=c(6.6))
print(predict(svm.model, irouzaki.X))

先ほどの学習効率がよくない状態のSVMにこのデータを食わせたら，両方とも0と出力された．つまり日本海側の堺も太平洋側と判断されてしまったことになる．

最初のテストデータの結果を見る限り，この4つの観測値，つまり降水量の合計，日照時間，平均風速，平均蒸気圧を使って太平洋側か日本海側を判別すると，太平洋側の都市を日本海側だと間違うことはあまりなく，日本海側の都市を太平洋側と間違うことが多いようだ．

つまり，1月の降水量，1月の日照時間，1月の風速平均，1月の湿度の4つの観測値は，日本海側と太平洋側を判定するのには不十分である，と言える．別の観測値を使って予測精度を上げてみよう．

Webブラウザ：Google Chromeのインストール

授業ではWebブラウザとしてGoogle Chromeを使うので，インストールしておく．

Google Chromeのページのページに行って，セットアップファイルをダウンロード，インストールしておく．