今回は,「気温以外のデータ」を使って,太平洋側の都市と日本海側の都市の分類器を作成してみる.
線形二項分類
線形分類(Linear Classification)とは,2つのカテゴリが入っているデータの集合の真ん中に一本直線を引くことで,カテゴリ分けする境目を定め,予測したいデータが入ってきた時に,どちらかに分類する問題である.もちろん人間が一本線を引くことで行うこともできるが,これを機械学習で行う.
入力するデータが2次元,例えば「降水量,日照時間」だった場合には,カテゴリ分けする境目は「直線」になるが,「降水量,日照時間,湿度」のように3次元になると「2次元平面」になり,「降水量,日照時間,湿度,風速」のように4次元だと「3次元超平面」になる.
3次元空間上の平面ぐらいは平面に表示するグラフでなんとか表示できるものの,4次元以上は無理なので,写像をするか「4次元の線形の式」として理解するしかない.
本項では,線形Support Vector Machine(Linear SVM)と,ロジスティック回帰(Logistic Regression)による,分類器というか,つまり直線に必要な「係数」および「切片」を学習する.
ロジスティック回帰は「回帰」と名がついているが,分類問題に使う.分ける直線を学習するので「線形回帰」とも言えるので,この名前がついている.
ダミー変数とカテゴリ変数
日本海側と太平洋側の年を分類すると書いたが,SVMやロジスティック回帰で機械学習するためには,これを数字に直さなければならない.もちろん太平洋側と日本海側は大小の比較ができないなど「値」としては,意味がないわけで,ここでは太平洋側を0,日本海側を1として表すことにする.
このように,その要素の有無で0と1の2値で表現される変数,その大小や差に意味がないものを「ダミー変数」と呼ぶ.(回帰分析でもダミー変数を使うことができる.)
例えば北海道の都市のように「太平洋側,日本海側,オホーツク海側」のように3つ以上の状態があり,2値で表すことができないもの,つまり「0, 1, 2, 3...などの状態が複数あり,かつその数字が大小の意味を持ってない場合」は,カテゴリ変数と呼ぶ
カテゴリ変数は二項分類つまりここでおこなような「AとBのどっち?」の問題では扱えないので,カテゴリ変数で表現している内容を,要素に分けて,要素の有無で表現,つまり複数のダミー変数に直すなどの方法をとる.
データの取得と加工
例によって,気象庁オープンデータのページから,
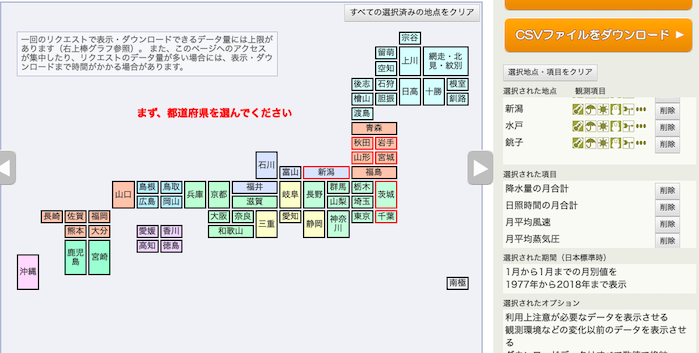
都市は,秋田県→秋田市,岩手県→宮古市,山形県→酒田市,宮城県→石巻市,新潟県→新潟市,茨城県→水戸市,千葉県→銚子市,の順で,それぞれ選択.
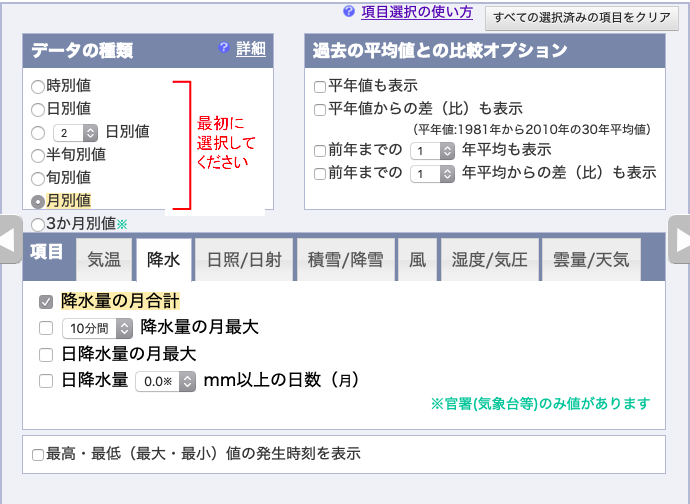
月別の値を選択し,降水量の月合計,
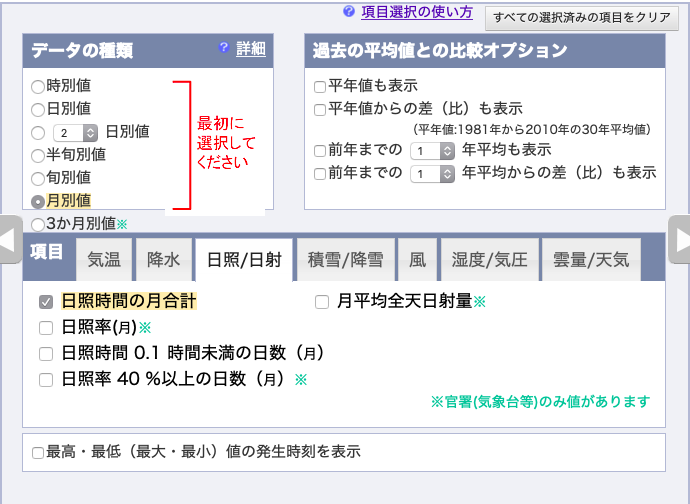
日照時間の月合計,
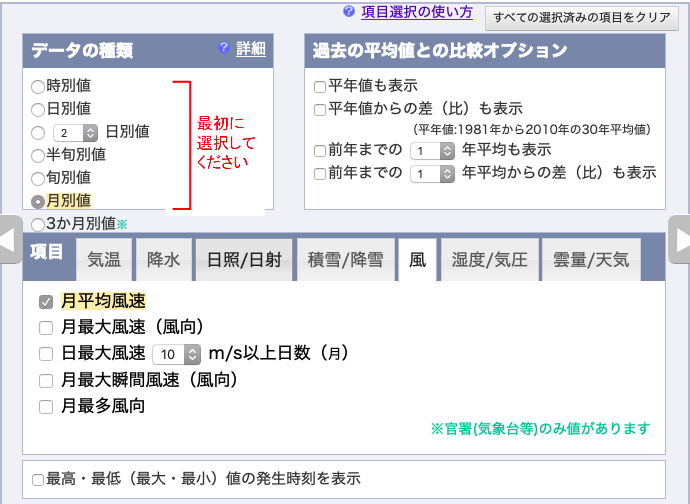
月平均風速,
湿度/気圧の月平均蒸気圧,を選択し,
1977年〜2018年の「1月」のデータをダウンロードする.
表示オプションはデフォルト.地点の順番と,項目の順番を確認すること.
ダウンロードしたCSVはこんな見た目になる.
このCSVを「太平洋側日本海側ダミー変数」を加えたスタック形式のデータに加工する.
Google Spreadsheetに上記CSVを読み込んだ状態.
例によって不要な行と列を削除する.降水量に関しては「現象なし情報」という列も含まれているので注意.
秋田, 宮古, 酒田, 石巻, 新潟, 水戸, 銚子を抽出するために新しいスプレッドシートのワークブックを作る.
ワークブック名とシート名を整える
変数名・列名を入れる.観測地点,太平洋側日本海側ダミー,降水量の合計,日照時間,平均風速,平均蒸気圧.
太平洋側日本海側ダミー変数は,太平洋側を0,日本海側を1と決めておく.
元のワークブックから,秋田の1977年〜2018年のデータを選択して,右クリック→コピー.
新しいワークブックの方の降水量のセルを指定して,右クリック→貼り付け.列の場所を間違えないように.
貼り付けられた状態.
観測地点列の頭に「秋田」を記入し,コピー.
その下,41行(残り41年分)の行の観測地点の列を選択して,貼り付け.
太平洋側日本海側ダミーの列に「1」を記入.前述のように太平洋側の都市が0で,日本海側の都市が1,秋田は「1」.コピー.
その下,41行(残り41年分)の行の太平洋側日本海側ダミーの列を選択して,貼り付け.
貼り付けられた状態.
同じように宮古(太平洋側),
酒田(日本海側),
石巻(太平洋側),
新潟(日本海側),
水戸(太平洋側),
銚子(太平洋側)のデータを作成する.
いつもと同じように,新しい方のワークブックのシートをファイル→ウェブに公開.
シートを,CSVとして公開する
Google Colabに読み込んで,pd.DataFrameとして読み込み最初の数行を表示.

目的変数Y(太平洋側日本海側ダミー)と,説明変数X(観測値)のnumpy配列に分けておく.
# 目的変数Yは「太平洋側か日本海側か」つまり,ダミー変数の列になる
y_whole = df.loc[:, '太平洋側日本海側ダミー']
# npの1次元配列に変換
y_whole = np.ravel(y_whole)
x_whole = df.loc[:, ['降水量の合計', '日照時間', '平均風速', '平均蒸気圧']]
# 目的変数Xは観測値4次元からなる.pd.DataFrameのまま使える.訓練データとテストデータ
前述の通り,線形二項分類は「データをうまく判別できるような直線を引く」ことで分類を行うが,これは言い換えれば,直線を表す式 y = ax + b のaとbを「機械学習」することである.
機械学習とは,自動的に「学習」の手順を定めて繰り返し行うことで,厳密ではないものの正解に近い解(近似解)に徐々に近づけていくことであるが,その時に訓練データ(トレーニングデータ)とテストデータの2つのデータセットを用いる.
訓練データを使って学習して,訓練データで表現される正解に近づいていくのは当然と言えば当然で,そこで学習の過程で「訓練データを使って学習して,テストデータでどれだけ正解に近いかを判別する」という流れを取る.そのために訓練データとテストデータは別のものにしておく必要がある.
とは言っても実際には「今持っているデータの半分を訓練データとして使い,残り半分をテストデータとして使うように指示する」だけである.スタック形式のデータが1000行分あれば,ランダムに500行抽出して訓練データとし,残り500行をテストデータにする,という形である.これはscikit-learnの中に入っている関数train_test_split関数で簡単にできる.
from sklearn.model_selection import train_test_split
# 関数を実行するだけで,ランダムに訓練データとテストデータを分けてくれる.
x_train, x_test, y_train, y_test = train_test_split(x_whole, y_whole)線形SVM
Support Vector Machine, SVMは,本来,非線形空間を線形に捻じ曲げて判別するためのものであり,今回のような最初から線形のものに使う意味はあまりないが,ごく基本的な線形分類学習機としても有効である.
scikit-learnで用意されているものは,大体この手順.まずモデルを呼び出しインスタンス化(実行可能な状態にする),fit関数に訓練データを与えて学習し,predict関数にテストデータを与えて,テストデータの方の予測値を出す.予測値と実際の値(ここでは太平洋側か日本海側か)をmetrics.accuracy_score関数に与え,正答率を出す,という流れ.
from sklearn.svm import LinearSVC
from sklearn import metrics
# モデルを呼び出して
svm_model = LinearSVC(C=1.0)
# fit関数に訓練データを入れて学習を実行する
svm_model.fit(x_train, y_train)
# predict関数にテストデータを入れて,学習結果をもとにテストデータを入れたときの「予測値」を計算する
svm_y_predict = svm_model.predict(x_test)
# テストデータの実際の値と予測値から正答率を計算する
svm_accuracy_score = metrics.accuracy_score(y_test, svm_y_predict)
print('svmの正答率', svm_accuracy_score)
# 係数がこの中に入っている.この係数で表される4次元空間の平面で切るとうまく分類できる,という意味
print('分離平面の係数', svm_model.coef_[0])
print('分離平面の切片', svm_model.intercept_[0])
# 分離平面の係数をもうちょっとわかりやすく表示してみる
x_labels = ['降水量の合計', '日照時間', '平均風速', '平均蒸気圧']
svm_coef_df = pd.DataFrame([x_labels, svm_model.coef_[0]]).T
# DataFrame.Tはnumpyのtransposeに相当し,配列の次元を入れ替える
print(svm_coef_df)結果は以下のようになる.訓練データとテストデータの分離やSVMの学習は,その時ごとに代わるので,必ずしもここまでいい結果が出るとは限らない.(というか,この結果は良すぎる)
svmの正答率 0.8648648648648649
分離平面の係数 [ 0.00037371 -0.01198279 0.3370101 -0.03095341]
分離平面の切片 0.05048275469556343
0 1
0 降水量の合計 0.000373713
1 日照時間 -0.0119828
2 平均風速 0.33701
3 平均蒸気圧 -0.0309534正答率は0.86とそこそこ高い.つまり4次元の空間上で,この傾きと切片により,直線(面というか立体というか)を引けば,ほぼ太平洋側と日本海側の都市を分離できる,ということになる.
ではさらに未知の都市,鳥取県境(日本海側)および静岡県石廊崎(太平洋側)の,2018年1月のデータを入れて,ちゃんと判別できるか見てみよう.
# 鳥取県境(日本海側),静岡県石廊崎(太平洋側)の2018年1月のデータを入れてみて,ちゃんと分類できるか検証する.
# 境のデータ 降水量191.5(mm), 日照時間58.1(時間), 平均風速2.6(m), 平均蒸気圧6.3(hPa),
# 石廊崎のデータ 降水量 93.5(mm), 日照時間188.6(時間), 平均風速6.8(m), 平均蒸気圧6.6(hPa)
sakaiX = np.array([[191.5, 58.1, 2.6, 6.3]], dtype=np.float)
irouzakiX = np.array([[93.5, 188.6, 6.8, 6.6]], dtype=np.float)
print('境の2018年1月のデータから予測した結果', svm_model.predict(sakaiX))
print('石廊崎の2018年1月のデータから予測した結果', svm_model.predict(irouzakiX))結果は以下の通り.
境の2018年1月のデータから予測した結果 [1.]
石廊崎の2018年1月のデータから予測した結果 [0.]6つ目のセルの結果は以下のようになる.境が1,石廊崎が0と判断されているので,学習したSVMの分類はそれなりに正しいようだ.もちろんさらに学習の精度を検証するために,他の都市,他の地点のデータを突っ込んで,確かめてみるのも良い.
ただしこれは「何回か学習を実行してかなり高い正答率になったSVMに突っ込んだ結果」である.実際には正答率の平均はもっと低い.結果を観察してみると,主に「太平洋側の都市を日本海側として間違えて判別する」例は少ないが,「日本海側の都市を太平洋側として間違えて判別する」例が多いようだ.
ロジスティック回帰
まったく同じデータを,ロジスティック回帰で分類の学習をしてみる.ロジスティック回帰は基本的に線形分類問題,つまり今回のように「直線を引くことで分類できる」問題に特化した手法である.
SVMと同じくscikit-learnに含まれているので,手順もSVMの時と全く同じである.モデルを読み込み,訓練データをfitし,テストデータをpredictして,正答率を出す.
from sklearn.linear_model import LogisticRegression
# X, Yの訓練データでロジスティック回帰を学習する
log_model = LogisticRegression()
log_model.fit(x_train, y_train)
# 学習済みのモデルにXテストデータをつっこみ,Yを予測し,観測データと比較
log_y_predict = log_model.predict(x_test)
log_accuracy_score = metrics.accuracy_score(y_test, log_y_predict)
print('ロジスティック回帰の正答率:', log_accuracy_score)
# 係数がこの中に入っている.この係数で表される4次元空間の平面で切るとうまく分類できる,という意味
print('分離平面の係数', log_model.coef_[0])
print('分離平面の切片', log_model.intercept_[0])
# 同じく分離平面の係数をもうちょっとわかりやすく表示してみる
log_coef_df = pd.DataFrame([x_labels, log_model.coef_[0]]).T
print(log_coef_df)実行結果は以下のようになる.ロジスティック回帰は何度学習を実行しても同じ結果が出る(内部的にニュートン法を使っている).ただし当然ながら訓練データとテストデータの分割を再度ランダムに行うと,結果は変わる.
ロジスティック回帰の正答率: 0.9682539682539683
分離平面の係数 [-0.00933651 -0.0580769 1.47516013 -1.16708297]
分離平面の切片 4.020109595993421
0 1
0 降水量の合計 -0.00933651
1 日照時間 -0.0580769
2 平均風速 1.47516
3 平均蒸気圧 -1.16708SVMの時と同じく,鳥取県境と静岡県石廊崎の2018年1月のデータから,太平洋側か日本海側かを予測させてみよう.
sakaiX = np.array([[191.5, 58.1, 2.6, 6.3]], dtype=np.float)
irouzakiX = np.array([[93.5, 188.6, 6.8, 6.6]], dtype=np.float)
print('境の2018年1月のデータから予測した結果', log_model.predict(sakaiX))
print('石廊崎の2018年1月のデータから予測した結果', log_model.predict(irouzakiX))結果は以下のようになる.
境の2018年1月のデータから予測した結果 [1.]
石廊崎の2018年1月のデータから予測した結果 [0.]ちゃんと分類できているが,やはり訓練データとテストデータの分け方によって予測精度にだいぶ差が出る.SVMの時と同じく,「日本海側の都市を誤って太平洋側」と判別している率が高い.
つまり,1月の降水量,1月の日照時間,1月の風速平均,1月の湿度の4つの観測値は,日本海側と太平洋側を判定するのには不十分である,と言える.別の観測値を使って予測精度を上げてみよう.