重回帰分析
重回帰分析とは,説明変数が2変数以上の回帰分析である.多変量解析と呼ばれる分析手法群の中の一つの手法である.重回帰分析は,モデルが線形である場合,つまり簡単に言えば「y = ax1 + bx2 + c」のaとbとcを求めることに相当する.さらに数を増やして「y = ax1 + bx2 + cx3 + dx4 + e」という式のa, b, c, d, eも求められる.
重回帰分析の時,モデルの中の説明変数x1やx2は,実は(x1)^2など二乗の場合でも分析できる.あくまで係数との関係が線形であれば線形回帰として求められる.この場合,説明変数を入力する際にあらかじめ二乗したデータを作っておいて,それを入力する作業が必要になる.
因果関係の推測
相関係数は,あくまで「相関」であり「因果」ではない,と相関係数の項で述べた.
重回帰分析は,線形回帰分析の項で述べた通り,p値を出してくれる.このp値は設定した説明変数ごとに算出されることになるが,このp値は何を言っているか,の帰無仮説と対立仮説は以下の通りである.
- 帰無仮説: この説明変数は,目的変数に影響を与えない.
- 対立仮説: この説明変数は,目的変数に影響を与える変数である.
つまり回帰分析は「因果関係」を推測するために使うことができる.
単純線形回帰分析なら変数が一つなのでそれほど問題はないのだが,重回帰分析の場合,観測できるデータを全て説明変数として回帰分析を行なっても,その変数が「疑似相関」すなわち「因果関係はないのに相関係数が高い」だけの場合もあり,疑似相関関係の変数が説明変数に含まれているときちんとした結果が出ない.
そこで重回帰分析では,「慎重に因果関係を考察,疑似相関と思われる説明変数を除いて,何度も説明変数をとっかえひっかえしながら,結果(主にp値)を見ていく」ことで,因果関係を推測する.
ダミー説明変数
例えば分散分析の群のように,数字で表すことができない説明変数があり,これで重回帰分析を行いたい時は,ダミー説明変数という考え方を使う.
ダミー変数は,グループなどを表す変数の中身を1と0で表すものである.サンプルがA群とB群の2つ(もしくはその属性を持っているか,いないか)だった場合は,説明変数1つで中身は1か0かの2択でよいが,3つの群があった場合「A群である:0or1」「B群である:0or1」「C群である:0or1」の3つの説明変数になることに注意.
データの取得と加工
単純線形回帰分析と同じと同じ気象庁オープンデータの八王子のものを使用するが,取ってくるデータは違う.
「地点を選ぶ」タブで,八王子を選択.
「項目を選ぶ」タブで,「月別値」を選択し,中の「気温」タブで「月平均気温」を選択
「降水」タブで,「降水量の月合計」を選択.
「日照・日射」タブで,「日照時間の月合計」を選択
「風」タブで,「月平均風速」を選択.
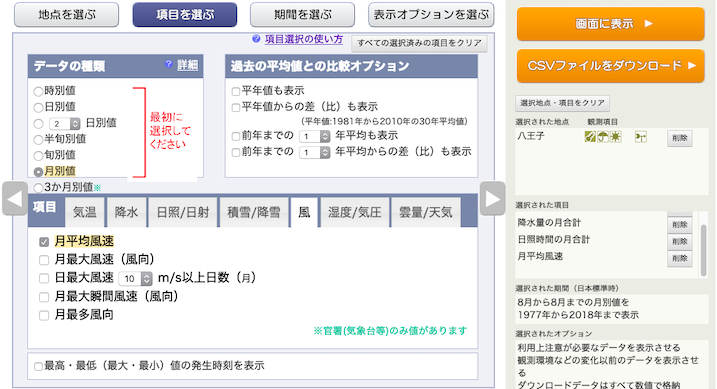
「期間」タブで,1977年〜2018年の8月を選択.
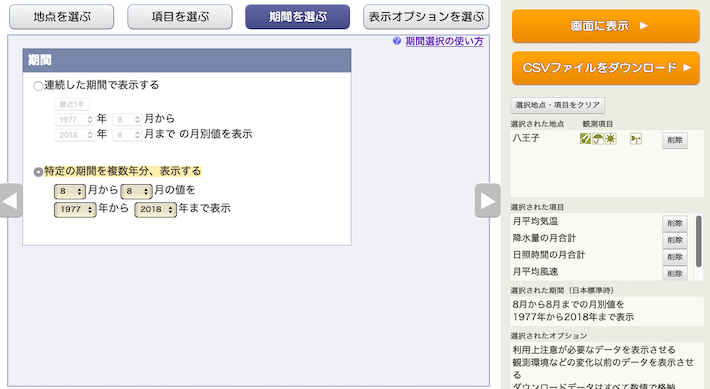
「CSVをダウンロード」し,Googleスプレッドシートで開く.
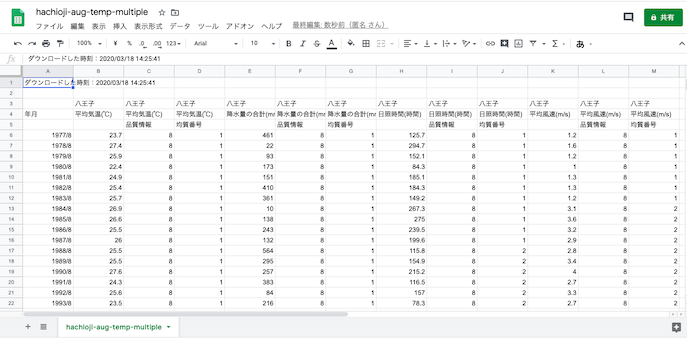
これまで通りに,不要な行と列を削除.今回は八王子だけなので,地点の行が不要な代わりに,平均気温等の項目を列名として用いるために残す.今回は年月もデータとしては食わせないので削除.
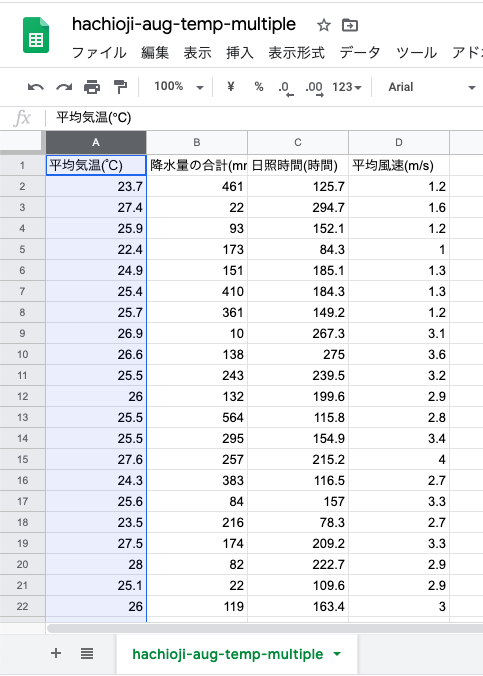
半角少かっこはRでは列名として読み込めないようなので,列名の行の少かっこに囲まれた単位を削除する.
この状態で,前回のようにWebにCSV形式で公開し,URLを取得しておく.
import numpy as np
import pandas as pd
df = pd.read_csv('公開したURL')
df.head()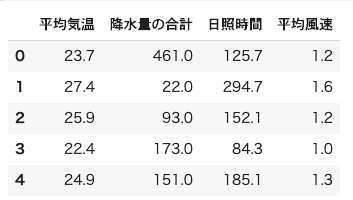
Scikit-Learnでの重回帰分析
説明変数の単純回帰分析と同じくScikit-Learnライブラリでは,説明変数が多い場合の重回帰分析を全く同じようにで行うことができる.違うのは説明変数の数であり,前回の単純回帰分析では説明変数,目的変数に与えるNumpy配列のshapeは,両方とも(41, 1)であった.
重回帰分析の場合,説明変数のshapeが説明変数の個数の分だけ大きくなる.
つまり,y = ax1 + bx2 + cx3 + d という式の, a, b, c, dを求めたい時の,説明変数のshapeは(41, 3)ということになる.
単純泉系回帰分析と全く同じなので,以下のようにする.
import scipy
import sklearn
from sklearn import linear_model
ols_model = linear_model.LinearRegression()
old_model.fit(説明変数の2次元配列のDataFrame, 目的変数の配列DataFrame)
print('回帰係数(傾き):', ols_model.coef_)
print('切片:', ols_model.intercept_)
print('決定係数', ols_model.score(X, Y))statsmodelsでの重回帰分析
statsmodelsを使う場合でも,単純線形回帰分析と全く同じように行う.
statsmodelsを使った分散分析でも回帰分析が出てくるが,分散分析で使った回帰分析の関数は,式を与えることにより線形以外も可能なものなので,線形のみを前提にしている場合,それとは別の簡単な方法つまり単純線形回帰のプログラムと全く同じプログラムで実行することができる.
import statsmodels.api as sm
ols_model = sm.OLS(目的変数のDataFrame, sm.add_constant(説明変数のDataFrame))
ols_result = ols_model.fit()
print(ols_result.summary())式を与える時は以下のようになる
import statsmodels.api as sm
import statsmodels.formula.api as smf
ols_model = smf.ols(formula='目的変数の列名 ~ 説明変数1の列名 + 説明変数2の列名 + 説明変数3の列名', data=全体のDataFrame)
ols_result = ols_model.fit()
print(ols_result.summary())この式は「Y(目的変数) = aX1(説明変数1) + bX2(説明変数2) + cX3(説明変数3) + d」を省略したものである.
Scipyと同じことができるが,前述の統計的因果推論に必要な情報は,statsmodelsの方が多いので,本項ではstatsmodelsの後者の方,つまり式を与える方を用いる.
DataFrameで複数の列を持ってくる
scipyを使う方法とstatsmodelsで式を与えない方法では,DataFrameから複数の列を1つのテーブルとして切り出したものを説明変数の観測値のセットとして与える必要がある.
単純泉系回帰分析では説明変数は1次元配列であり,プログラム上は無理やり2次元配列にしたものをモデルに食わせるが,重回帰分析では説明変数が最初から2次元配列である.
CSVを読み込んだ後2次元配列テーブルを取り出す方法は,「「列の名前」をカンマで区切った配列」を使えば取得できる.
df = pandas.read_csv('CSVファイル名')
df = df.loc[:, ['平均気温(℃)', '日最高気温の平均(℃)']]
とすれば,平均気温の列と日最高気温の平均の2つの説明変数を格納したDataFrameができ,このDataFrameのshapeは(41, 2)となる.
statsmodelsで式を与える場合のコード例
読み込んだDataFrameを,目的変数に「平均気温」,説明変数に「降水量の合計」「日照時間」「平均風速」の3つと設定し,式を与えるstatsmodelsのモデルを使って重回帰分析を行う.
コードは以下のようになる.
import statsmodels.api as sm
import statsmodels.formula.api as smf
ols_model = smf.ols(formula='平均気温 ~ 降水量の合計 + 日照時間 + 平均風速', data=df)
ols_result = ols_model.fit()
print(ols_result.summary())結果は以下のようになる.
OLS Regression Results
==============================================================================
Dep. Variable: 平均気温 R-squared: 0.636
Model: OLS Adj. R-squared: 0.607
Method: Least Squares F-statistic: 22.10
Date: Fri, 03 Apr 2020 Prob (F-statistic): 1.89e-08
Time: 07:35:43 Log-Likelihood: -48.103
No. Observations: 42 AIC: 104.2
Df Residuals: 38 BIC: 111.2
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 22.2742 0.643 34.648 0.000 20.973 23.576
降水量の合計 -0.0003 0.001 -0.403 0.689 -0.002 0.001
日照時間 0.0138 0.003 5.393 0.000 0.009 0.019
平均風速 0.5611 0.175 3.209 0.003 0.207 0.915
==============================================================================
Omnibus: 2.936 Durbin-Watson: 1.391
Prob(Omnibus): 0.230 Jarque-Bera (JB): 2.701
Skew: -0.552 Prob(JB): 0.259
Kurtosis: 2.431 Cond. No. 1.62e+03
==============================================================================考察と再度の実行
単純線形回帰分析と同じく,Interceptのcoefが欠片で,他の説明変数のcoefが傾きになる.つまりこの結果は,
「8月の月平均気温 = -0.0003*降水量の月合計 + 0.0138*日照時間の月合計 + 0.05611*月平均風速 + 22.2742」を表している.
結果を見ると,降水量の傾きが非常に小さいことから,降水量は月平均気温にほとんど影響を与えていないことがわかる.実際にp値(Pr>|t|で表示されている)を見てみると,0.05を超えている.
回帰分析のp値の意味を思い出してみると,帰無仮説:「説明変数は目的変数に影響を与えている」,対立仮説:「説明変数は目的変数に影響を与えているとは言えない」であった.
降水量のp値は0.05を大きく超えているので,「(八王子の場合)8月の降水量は月平均気温には影響を与えているとは言えない」と言うことができる.
では,降水量のデータを外して,再度重回帰分析をしてみよう.
目的変数は月平均気温まので変える必要がなく,元のpandas.DataFrameから抽出する列名指定を変えるだけである.
# 降水量を外して,再度重回帰分析を行う
import statsmodels.api as sm
import statsmodels.formula.api as smf
ols_model = smf.ols(formula='平均気温 ~ 日照時間 + 平均風速', data=df)
ols_result = ols_model.fit()
print(ols_result.summary())結果は以下のようになる.
OLS Regression Results
==============================================================================
Dep. Variable: 平均気温 R-squared: 0.634
Model: OLS Adj. R-squared: 0.615
Method: Least Squares F-statistic: 33.79
Date: Fri, 03 Apr 2020 Prob (F-statistic): 3.06e-09
Time: 07:41:07 Log-Likelihood: -48.192
No. Observations: 42 AIC: 102.4
Df Residuals: 39 BIC: 107.6
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 22.1272 0.524 42.254 0.000 21.068 23.186
日照時間 0.0142 0.002 6.124 0.000 0.010 0.019
平均風速 0.5605 0.173 3.240 0.002 0.211 0.910
==============================================================================
Omnibus: 2.704 Durbin-Watson: 1.376
Prob(Omnibus): 0.259 Jarque-Bera (JB): 2.495
Skew: -0.527 Prob(JB): 0.287
Kurtosis: 2.439 Cond. No. 788.
==============================================================================降水量を外して計算したので,先ほどとは値が多少違っているが,無事に全てp値が低い値に収まっており,「日照時間と平均風速は月平均気温に影響を与えている」と言うことができる.
面白いのは,傾きが小さい日照時間の方がp値が小さいことである.これは単位というか物理量の違いがあるため.日照時間は「月に何時間日照があったか」という月の延時間,平均風速は気象庁オープンデータの場合「10分ごとの風速の月平均」であることから,傾きが違うのは当然とも言える.
重回帰分析の面白いところは,このように単位が異なっても,また前述のように「ダミー変数」を用いたとしても結果がでることである.ダミー変数は単位すらなく,0か1の値しか取らないが,p値をみることで「それが影響を与えているかどうか」をみることができる.重回帰分析の目的は,この「傾きを出す」ことではなく,p値を見て「影響を与えているか」を探ることである.
「日照時間が気温に影響を与えること」は明白であり,さらにp値も十分に低いことから,日照時間と月の平均気温の間には因果関係があると言っても良いだろう.
さらに「風が強くなると気温に大きく影響を与える」ことが統計的に示されたが,直接の因果関係があるとは考えづらく,間にならんらかの要素を挟んでいる(例えば日照時間に影響を与える雲の量は風速によって影響を受ける)と考えられる.
つまり,p値が直接因果関係を示すわけではなく「因果関係を考えるために統計的なp値を使う」ことができる.
結果のR-squaredという項目を見てみよう.0.634という値が表示されているが,これはR^2(Rの2乗)やR2という形でよくかかれる「決定係数」というものである.決定係数は「この得られた数式が,観測した値にどれだけフィットしているか」を表す値であり,0〜1の範囲を取り,1であれば非常にフィットしている,0であれば全くフィットしていない,という意味である.
例えば「p値は高いが,R^2が極端に低い時」には,lm関数に与えるformula,つまり式(「モデル」と呼ぶ)を見直してやると良い.今回与えたのは単純な線形多項式であるが,実は説明変数の2乗の項が含まれている二次関数かもしれない.
決定係数が0.5以下だと,数式が大幅に間違っているという判断をされることが多い.
課題
自身の身近な題材を取り上げ,データを取得,相関係数を算出,それを元に線形モデルを立て重回帰分析を行い,因果関係を推測せよ.