こーひーをぶんなぐれ！ - CSVデータからの相関係数の算出

本項でもGoogle Colaboratoryを使用する．（もちろんファイル読み込みの部分以外はJupyter Notebookでもよいし，一気にPythonのソースコードをまとめて書いて実行しても問題はない）

相関係数

JISでは，相関のことを「2つの確率変数の分布法則の関係．多くの場合線形関係の程度を指す」と定義している．

要するに，比例関係にありそうな2つの軸による「2つの値のペア」が大量にあり，それをざっとみた時，どのぐらい比例関係（もしくは反比例関係）の直線上に載っているか，を示す値が「相関係数」である．

相関係数は-1から1の間を取り，1の時観測データは比例の一直線上に並ぶ．-1のときは反比例の一直線上に並ぶ．（ちなみに，相関係数0とは，傾きが全くない一直線上に並ぶことを示すが，ほとんどの場合相関係数は算出できない）

実世界の観測データには常にノイズが載っていて一直線上に並ぶことはありえないので，相関係数が1や-1というのはありえないのだが，1や-1に近いほど「線形モデルに理想的に近い」ということができる．

上図が，観測値の数（サンプル数）が多い時の，相関係数に従った分布のイメージである．

相関係数が高いほど比例の直線に綺麗に載るようになり，逆に低いほどバラつきがある．自然現象は「正規分布」という分布に従うことが多いが，サンプル数が多いとこのようにグラフ上で綺麗に見ることができる．逆にサンプル数が少ない時はグラフに表示してもぱっと見ではわからない．そこで「観測された値は正規分布に従う」前提で相関係数を出して，サンプル数が少ない時でも全体のばらつきを「相関係数」として知ることができるようになる．

相関係数が-1.0から0までの負の値の時は，反比例の直線が基準になる．

本項では，「緯度（北緯）が大きければ大きいほど，つまり北の観測地点ほど，8月の気温が低くなる，緯度と8月の気温に負の相関がある，と仮定し，その相関係数を確かめる．

気象庁オープンデータ

「気象庁|過去の気象データ・ダウンロード」ページから，必要なデータを絞ってCSV形式でダウンロードすることができる．これを分析対象にする．

官公庁らしく，文字コードがSHIFT-JISなので注意する．

東日本の県庁所在地の「1977年〜2018年の，8月の平均気温，8月の日最高気温の平均，8月の日最低気温の平均，8月で日平均気温が25℃を上回った日数」のデータを落としてくる．手順は以下の通り．

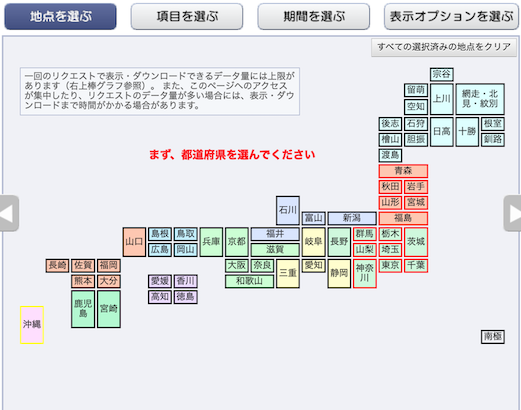
まず観測地点を選ぶ．東日本の各県をクリックし，その中で県庁所在地を選択しておく．

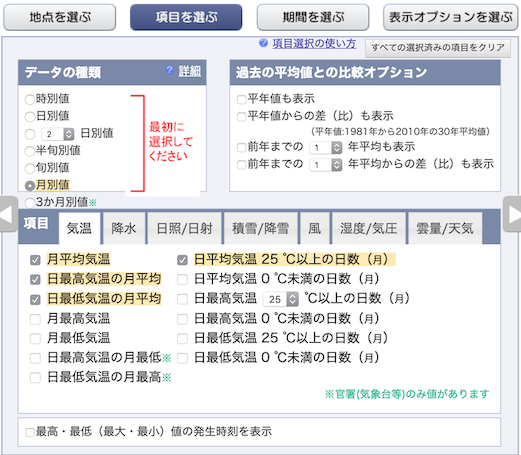
次にデータの種類を選ぶ．「データの種類」は「月別値」，「項目」は「気温」「日最高気温の月平均」「日最低気温の月平均」「日平均気温が25℃を超えた日数」を選択する．

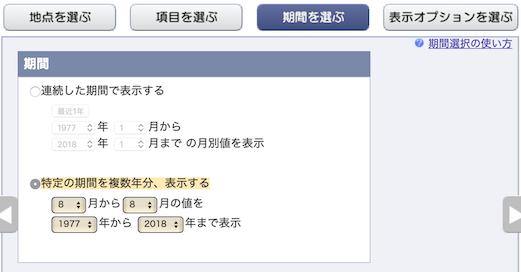
「期間」は，「8月から8月」「1977年〜2018年」つまり，各年の8月のデータだけを持ってくる．

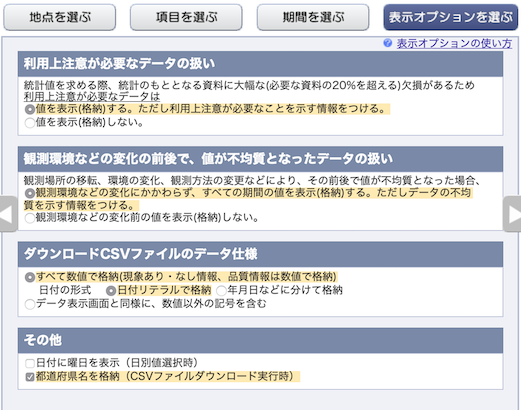
表示オプションは「都道府県名を格納」にチェックを入れておく．

この状態で，右の「CSVをダウンロード」する．

ちなみにダウンロードしたデータはこのようになる．

コード例

1つ目のセル．実行してGoogle Colab上にファイルをアップロードする．

from google.colab import files
uploaded = files.upload()

1つ目のセルの実行結果は以下のようになる．

2つ目のセル．CSVファイルを読み込み，DataFrame形式にする．

import numpy as np
import pandas as pd
from pandas import Series, DataFrame

# DataFrameの変数はdfにするのが一般的
df = pd.read_csv('tohoku-kanto-aug.csv', encoding='SHIFT-JIS', header=2)
# headerは2行読み飛ばす，という意味
# エディタで確認するとわかる通り，余計なものが入っているので

# 頭から数行，数列を見せてくれる．
# Google Colaboratoryの場合，セルの最後で実行すると，綺麗に色分けして見せてくれる
# 途中で実行する場合には，　print(df.head()) とすること．
df.head()

2つ目のセルの実行結果は以下のようになる．

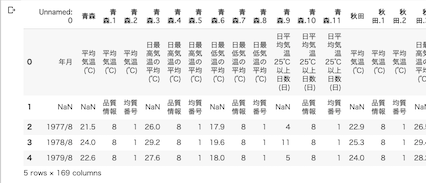
3つ目のセルは以下の通り．不要な「列」を落としていく．

# DataFrameでは，この状態で一番上の行が「列の名前」として認識され，操作することができる．
# 列の名前になっているので，この行を行番号では操作できなくなる．

# for文で余計な「列」を削除する
# 品質情報，均質番号の列がいらない
# 青森であれば，青森1, 2, 4, 5, 7, 8, 10, 11がいらない

for a_column in ['青森', '秋田', '盛岡', '山形', '仙台', '福島', '水戸', '宇都宮', 'さいたま', '前橋', '甲府', '千葉', '東京', '横浜']:
  for i in range(1, 11, 3):
    for j in range(0, 2, 1):
      df = df.drop(a_column + '.' + str(i + j), axis=1)

      # dropの時に行番号や列番号，行の名前や列の名前をいれるが，
      # 標準だと「行」の削除が行われれ，
      # axis=1というオプションを入れると「列」で削除が行われる

df.head()

3つ目のセルの実行結果は以下のようになる．品質情報と均質番号の列がいらないので，削除する．

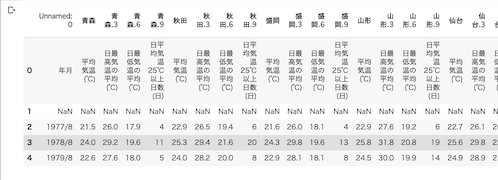
4つ目のセルは以下の通り．品質情報と均質番号があった行を削除する．

# 1行目 (0行目ではなく)が余計なので削除しておく
df = df.drop(1)

# 再度確認
df.head()

4つ目のセルの実行結果は以下の通り．

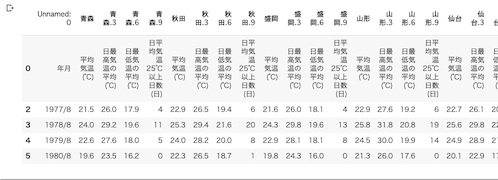
5つ目のセルは以下の通り．今回は年月は関係ないので，年月の列を落として，中身のデータのプレーンな状態（つまりnumpy配列）を確認し，形状を確認する．

# 「地名」の列は8月の平均気温，
# 「地名.3」の列は8月の日最高気温の平均
# 「地名.6」の列は8月の日最低気温の平均
# 「地名.9」の列は8月の日平均気温が25℃以上の日数
# を記録したら，その説明が入っている0行目と，年月が入っている0列目を削除

df = df.drop(0)
df = df.drop('Unnamed: 0', axis=1)

# データを確認．dataframeの中のvaluesという変数に入っている
print(df.values)

# shapeつまり次元を確認．
print(df.values.shape)

5つ目のセルの実行結果は以下の通り．42年分（行）のデータが14地点分*4=56（列，8月の平均気温，8月の日最高気温，8月の日最低気温，平均気温が25℃を上回った日数で*4）入っている．

[['21.5' '26.0' '17.9' ... '27.7' '21.8' '15']
 ['24.0' '29.2' '19.6' ... '32.1' '24.8' '31']
 ['22.6' '27.6' '18.0' ... '30.5' '24.0' '25']
 ...
 ['24.5' '28.7' '21.0' ... '31.3' '24.5' '29']
 ['22.0' '26.3' '18.9' ... '30.4' '24.0' '22']
 ['22.8' '27.4' '19.3' ... '32.1' '25.3' '26']]
(42, 56)

6つ目のセルは以下の通り．今回は緯度との相関係数を求めるので，各観測地点の緯度（longitude）を調べて，その配列を作る．まず青森から．

# 42年分のデータがある

# 緯度の配列を作成して，対応させる
# 青森の8月の平均気温を1次元配列として取り出して，数字の配列にする
aomori_ave = df.loc[:, '青森'].values.astype('float32')
# locは行と列を指定して，配列として取り出す 
# :は0~あるだけ，という意味
# つまり行は0~あるだけ（42年分) 列は'青森'を取り出したということ
# そのあとnumpy配列にするため，valuesを使い，さらに文字列から数字に変更している
print('青森市の8月の平均気温42年分', aomori_ave)

# 青森市は北緯40.49度
aomori_longi = np.repeat(40.49, 42)
# 40.49を42年分繰り返した配列を作る
print('青森市の8月の緯度42年分', aomori_longi)

#当たり前だが，何月だろうと何年だろうと，緯度は変わらないので，同じ数字が続く配列になる．

6つ目のセルの実行結果は以下の通り．確認する．

青森市の8月の平均気温42年分 [21.5 24.  22.6 19.6 22.1 23.5 23.8 24.5 25.7 22.7 21.8 23.3 23.8 24.5
 21.5 22.5 20.6 25.9 23.6 22.2 22.7 22.  25.8 24.8 21.4 21.9 21.3 23.1
 24.9 24.4 24.6 21.9 21.9 26.  24.2 25.3 24.7 23.6 23.6 24.5 22.  22.8]
青森市の8月の緯度42年分 [40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
 40.49 40.49 40.49 40.49 40.49 40.49]

7つ目のセルは以下の通り．とりあえず青森だけを散布図としてグラフ描画してみる．横軸が緯度，縦軸が「気温」

# 散布図として描画する
import matplotlib.pyplot as plt
plt.scatter(aomori_longi, aomori_ave, label='Aomori')
#判例を表示する
plt.legend()
plt.show()

7つ目のセルの実行結果は以下の通り．横軸が緯度で，青森だけのデータなので，自然に縦に1直線に並ぶことになる．

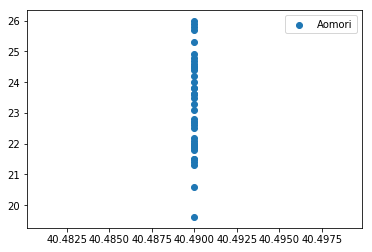
8つ目のセルは以下の通り．青森が大丈夫そうなので，他の地点も全部緯度配列を作り，描画する．一度plt.show()するとグラフの中身は初期化されるので，再度青森から追加していく．

# 同様に盛岡，仙台，福島，水戸，千葉，東京の太平洋側の県庁所在地各地についても行い，散布図として追加描画する
# セルが違う = 描画されるグラフが違うので，まず青森を再描画する
plt.scatter(aomori_longi, aomori_ave, label='Aomori')

# 盛岡以南
morioka_ave = df.loc[:, '盛岡'].values.astype('float32')
morioka_longi = np.repeat(39.42, 42) #盛岡市は北緯39.42
plt.scatter(morioka_longi, morioka_ave, label='Morioka')

sendai_ave = df.loc[:, '仙台'].values.astype('float32')
sendai_longi = np.repeat(38.16, 42) #仙台市は北緯38.16
plt.scatter(sendai_longi, sendai_ave, label='Sendai')

fukushima_ave = df.loc[:, '福島'].values.astype('float32')
fukushima_longi = np.repeat(37.45, 42) #福島市は北緯37.45
plt.scatter(fukushima_longi, fukushima_ave, label='Fukushima')

mito_ave = df.loc[:, '水戸'].values.astype('float32')
mito_longi = np.repeat(36.22, 42) #水戸市は北緯36．22
plt.scatter(mito_longi, mito_ave, label='Mito')

tokyo_ave = df.loc[:, '東京'].values.astype('float32')
tokyo_longi = np.repeat(35.41, 42) #千代田区役所は北緯35.41
plt.scatter(tokyo_longi, tokyo_ave, label='Tokyo')

chiba_ave = df.loc[:, '千葉'].values.astype('float32')
chiba_longi = np.repeat(35.36, 42) #千葉市は北緯35.36
plt.scatter(chiba_longi, chiba_ave, label='Chiba')

plt.legend()
plt.show()

8つ目のセルの実行結果は以下の通り．観測地点ごとに1直線に並ぶ．

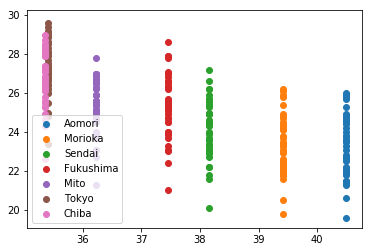
既に「なんとなく気温は緯度に反比例しているんじゃないかなぁ」はわかるが，幅が大きい．

9つ目のセルは以下の通り．緯度と8月の平均気温の相関係数を計算する．

相関係数の計算はpandasの機能を使う．そのためnumpy1次元配列をPandasのSeriesに変換する必要がある．DataFrameがpandasの2次元配列で，Seriesがpandasの1次元配列だと考えるとわかりやすい．

緯度と気温のペアになるように，緯度と気温の配列をそれぞれ全て連結する．散布図を書いていることからわかるように，相関係数を計算するときはペアになっていればペア間の並びは順不同で良い．

# さてここまでできたら，緯度と8月の平均気温の相関を計算する

# 北から順番に8月の平均気温配列と，緯度配列を連携つしていく．
# 順番を間違えると，緯度と気温の対応が取れなくなる
all_point_ave = np.concatenate([aomori_ave, morioka_ave, sendai_ave, fukushima_ave, mito_ave, tokyo_ave, chiba_ave])
all_point_longi = np.concatenate([aomori_longi, morioka_longi, sendai_longi, fukushima_longi, mito_longi, tokyo_longi, chiba_longi])

# pandasのSeriesに変換する
# pandasの2次元の表がDataFrameで，1次元配列がSeries
all_point_ave_series = pd.Series(all_point_ave)
all_point_longi_series = pd.Series(all_point_longi)

# 相関を計算する
correlation_coefficient = all_point_longi_series.corr(all_point_ave_series)

print('東日本の太平洋側の都市の緯度と8月の平均気温の相関係数は', correlation_coefficient)

9つ目のセルの実行結果は以下の通り．

東日本の太平洋側の都市の緯度と8月の平均気温の相関係数は -0.6768226395347305

相関係数が-0.677．相関係数は1〜0〜-1の値をとるので，-0.677は結構高めの負の相関があることになる．

負の相関は反比例を表す．前述の通り緯度が大きくなればなるほど，8月の平均気温が低くなるので，間違ってはいない．

相関係数は，あくまで相関の度合いなので，相関係数だけで全ての説明できるわけではないが，同じく8月の日最高気温，日最低気温，日平均気温25℃以上の日数についても，緯度に対する相関係数を算出して比較することには意味がある．ので他の気温についても相関係数が高いものを見つける．

10番目のセルは以下の通り．

# 8月の日最高気温の平均，8月の日最低気温の平均，25度以上の日数をそれぞれ格納する
aomori_max_ave = df.loc[:, '青森.3'].values.astype('float32')
aomori_min_ave = df.loc[:, '青森.6'].values.astype('float32')
aomori_count_25over = df.loc[:, '青森.9'].values.astype('uint8') #日数は0もしくは正の整数なので

morioka_max_ave = df.loc[:, '盛岡.3'].values.astype('float32')
morioka_min_ave = df.loc[:, '盛岡.6'].values.astype('float32')
morioka_count_25over = df.loc[:, '盛岡.9'].values.astype('uint8')

sendai_max_ave = df.loc[:, '仙台.3'].values.astype('float32')
sendai_min_ave = df.loc[:, '仙台.6'].values.astype('float32')
sendai_count_25over = df.loc[:, '仙台.9'].values.astype('uint8')

fukushima_max_ave = df.loc[:, '福島.3'].values.astype('float32')
fukushima_min_ave = df.loc[:, '福島.6'].values.astype('float32')
fukushima_count_25over = df.loc[:, '福島.9'].values.astype('uint8')

mito_max_ave = df.loc[:, '水戸.3'].values.astype('float32')
mito_min_ave = df.loc[:, '水戸.6'].values.astype('float32')
mito_count_25over = df.loc[:, '水戸.9'].values.astype('uint8')

tokyo_max_ave = df.loc[:, '東京.3'].values.astype('float32')
tokyo_min_ave = df.loc[:, '東京.6'].values.astype('float32')
tokyo_count_25over = df.loc[:, '東京.9'].values.astype('uint8')

chiba_max_ave = df.loc[:, '千葉.3'].values.astype('float32')
chiba_min_ave = df.loc[:, '千葉.6'].values.astype('float32')
chiba_count_25over = df.loc[:, '千葉.9'].values.astype('uint8')

# 連結する
all_point_max_ave = np.concatenate([aomori_max_ave, morioka_max_ave, sendai_max_ave, fukushima_max_ave, mito_max_ave, tokyo_max_ave, chiba_max_ave])
all_point_min_ave = np.concatenate([aomori_min_ave, morioka_min_ave, sendai_min_ave, fukushima_min_ave, mito_min_ave, tokyo_min_ave, chiba_min_ave])
all_point_count_25over = np.concatenate([aomori_count_25over, morioka_count_25over, sendai_count_25over, fukushima_count_25over, mito_count_25over, tokyo_count_25over, chiba_count_25over])

# pandasのSeriesに変換
all_point_max_ave_series = pd.Series(all_point_max_ave)
all_point_min_ave_series = pd.Series(all_point_min_ave)
all_point_count_25over_series = pd.Series(all_point_count_25over)

# 相関係数を出す
coefficient_max_ave = all_point_longi_series.corr(all_point_max_ave_series)
coefficient_min_ave = all_point_longi_series.corr(all_point_min_ave_series)
coefficient_count_25over = all_point_longi_series.corr(all_point_count_25over_series)

print('東日本の太平洋側の都市の緯度と8月の日最高気温平均の相関係数は', coefficient_max_ave)
print('東日本の太平洋側の都市の緯度と8月の日最低気温平均の相関係数は', coefficient_min_ave)
print('東日本の太平洋側の都市の緯度と8月の25℃を超えた日数の相関係数は', coefficient_count_25over)

10個目のセルの実行結果は以下の通り．

東日本の太平洋側の都市の緯度と8月の日最高気温平均の相関係数は -0.5206503321172122
東日本の太平洋側の都市の緯度と8月の日最低気温平均の相関係数は -0.7595445362207282
東日本の太平洋側の都市の緯度と8月の25℃を超えた日数の相関係数は -0.6830720670305753

結果を見ると，緯度との相関が一番強いのは「日最低気温の月平均」であることがわかった．つまり「最高気温と緯度との関係よりも，気温が下がりづらいことと緯度の関係が強い」ということである．

ただし相関係数はあくまで相関であり，因果関係ではない．因果を統計的に説明する必要があるので，次の線形回帰分析，重回帰分析を行う必要がある．