こーひーをぶんなぐれ！ - CSVデータからの主成分分析

本項でもGoogle Colaboratoryを使用する．（もちろんファイル読み込みの部分以外はJupyter Notebookでもよいし，一気にPythonのソースコードをまとめて書いて実行しても問題はない）

主成分分析

これまで「8月の平均気温」「8月の日最高気温の月平均」「8月の日最低気温の月平均」「25度を超えた日数」という4つの観測値を扱ってきた．この「4つの観測値から『都市の気候』をうまく表現したい．うまく説明できるようにしたい．」という問題を考える．

ところが，観測値が4つある時，つまり説明変数が4つある時，2次元グラフはそれぞれの軸の組み合わせて6通り存在する．さらに3つ以上の観測値を軸にして見ることはできないため，グラフでぱっと見ではわからない．

そこで「主成分分析」という「次元削減」手法を用いる．

主成分分析は，説明変数が多数存在する時に，元のデータの特徴を十分に表しつつ，かつ次元が少ない説明変数のセットを「合成」する手法である．

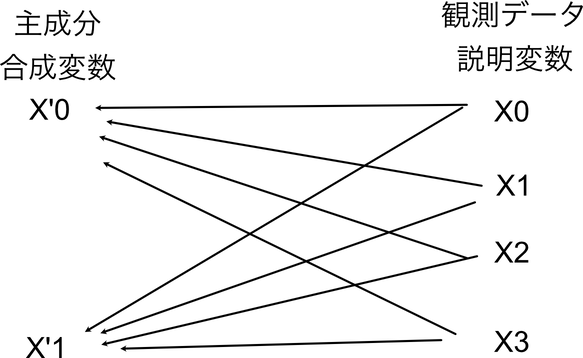
実際のには，上図のようにただ足し合わせるだけではなく，変換行列を作成し，それによって次元削減をするが，その変換行列を作成する際に「元のデータの特徴を十分に表現できる」ことを目標として調整をしていく．

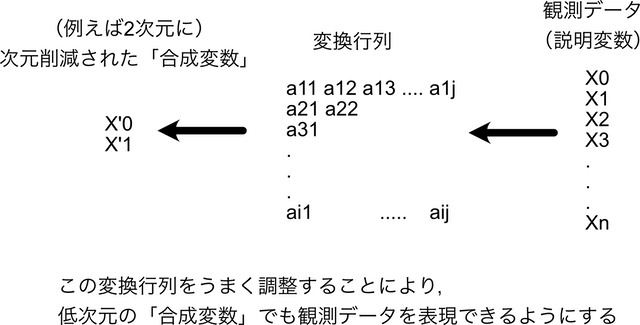
これは3DCGのレンダリングの時の3次元座標から2次元座標の変換行列（カメラの位置，アングル，拡大度等から算出される）を「3Dモデルのディティールが上手く掴める」ように調整するのに，イメージ的には近い．

十分に表現できるような「カメラの位置」「カメラの角度」「画角」「拡大」などをうまく調整し，3Dデータの特徴を十分に表現できるような2次元画像にするのと，主成分分析のための変換行列の作成は，似たようなもんである．

使用するデータ

今回はデータとして，相関係数を出した時と同じ「東日本の県庁所在地」の「1977年〜2018年」の「8月の平均気温」「8月の日最高気温の月平均」「8月の日最低気温の月平均」「25度を超えた日数」のCSVファイルを使う．

コード例

1つ目のセルはいつもの通り，CSVをGoogle Colaboにアップロードする．

from google.colab import files
uploaded = files.upload()

2つ目のセルでは，相関係数を出した時と同じく，抜き出してDataFrameを構築する．

import numpy as np
import pandas as pd
from pandas import Series, DataFrame

df = pd.read_csv('tohoku-kanto-aug.csv', encoding='SHIFT-JIS', header=2)
# 前と同じ処理をして，抜き出しておく
for a_column in ['青森', '秋田', '盛岡', '山形', '仙台', '福島', '水戸', '宇都宮', 'さいたま', '前橋', '甲府', '千葉', '東京', '横浜']:
  for i in range(1, 11, 3):
    for j in range(0, 2, 1):
      df = df.drop(a_column + '.' + str(i + j), axis=1)

df = df.drop(1)

# DataFrameの中に欠損値がある場合は，0.0を代わりに入れておく
df = df.fillna(0)
df.head()

2つ目のセルの実行結果は以下のようになる．

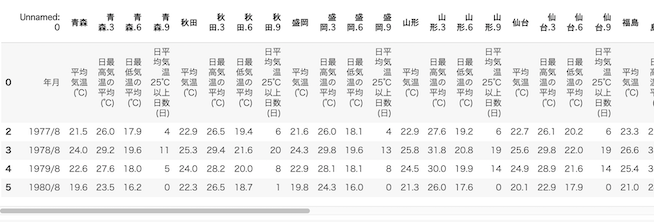
3つ目のセルでは，その中から3つの都市を抜き出して，重回帰分析の項でやったようなスタック形式のデータを構築する．

全てのデータを変数ごとに配列につないで，順列に並んだデータフレームを構築する．ついでに都市名ラベルの列も作ってくっつけておく．そして全ての配列をvstack関数で繋ぐ．（vertical stack，つまり垂直方向にスタックする，の意味）

vstackしただけだと，想定とは逆に重なってしまうので，transposeして，配列の次元を入れ替えておく．

今回は，盛岡，甲府，横浜を選んだ．

# グラフ表示するためにローマ字ラベルを作っておく
all_city_list = (['Aomori', 'Akita', 'Morioka', 'Yamagata', 'Sendai', 'Fukushima', 'Mito', 'Utsunomiya', 'Saitama', 'Maebashi', 'Kofu', 'Chiba', 'Tokyo', 'Yokohama'])

# 盛岡，甲府，横浜を選ぶ
choosed_cities = (['Morioka', 'Kofu', 'Yokohama'])

# 選んだ都市の
# average_temp: 8月の平均気温
# max_average_temp: 8月の最高気温の月平均
# min_avaerage_temp: 8月の最低気温の月平均
# num_of_days_25over: 
# として，それぞれ42年分を，1つ配列としてくっつける

# 選んだ3都市の42年分のラベルを繋げておく　(42年分*3都市)
city_label = np.array(choosed_cities)
city_label = np.repeat(city_label, 42)

# データをつなげる
# まず最初に空の配列を作っておいて，
average_temp = np.array([])
max_average_temp = np.array([])
min_average_temp = np.array([])
num_of_days_25over = np.array([])

# 選んだ都市の，8月の平均気温，最高気温の月平均，最低気温の月平均，25度を超えた日数を
# それぞれ1つの配列につなぐ
for a_city in choosed_cities:
  i = all_city_list.index(a_city)
  average_temp = np.concatenate((average_temp, df.iloc[1:, 1+i*4]))
  max_average_temp = np.concatenate((max_average_temp, df.iloc[1:, 1+i*4+1]))
  min_average_temp = np.concatenate((min_average_temp, df.iloc[1:, 1+i*4+2]))
  num_of_days_25over = np.concatenate((num_of_days_25over, df.iloc[1:, 1+i*4+3]))

# vstackで重ねて，配列の次元を入れ替えて，DataFrameにしておく
df_X1 = pd.DataFrame(np.vstack([city_label, average_temp, max_average_temp, min_average_temp, num_of_days_25over]).transpose())
# DataFrameの列名をつけておく
df_X1 = df_X1.rename(columns={0: '都市名', 1:'8月の平均気温', 2:'8月の日最高気温の月平均', 3:'8月の日最低気温の月平均', 4:'25度を超えた日数'})
# DataFrameの冒頭を確認
df_X1.head()

3つ目のセルの実行結果は以下の通りである．

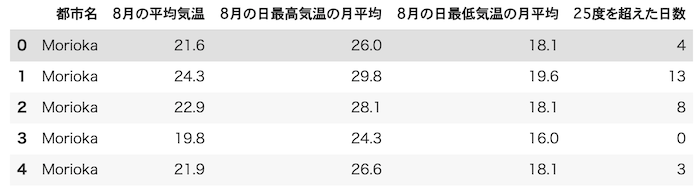
4つ目のセルでは，説明変数4つをx軸とy軸に取り，2次元のグラフを描画している．説明変数の組み合わせは合計6通りあるが，とりあえず3つの組み合わせでグラフを描画する．

# 生データを散布図でプロットしてみる
# 説明変数が4つで2次元に表示するためには，6通りのxとyの組み合わせがあるが，とりあえず3つだけ
import matplotlib.pyplot as plt

# 都市名ラベルの0番目を除いた説明変数4つ分で3つのグラフを描く
for i in range(1, 4, 1):
  for j, a_city in enumerate(choosed_cities):
    # 42年分 * 3都市分なので，都市ごとに色を変えるため，データを分けてscatterを呼び出す
    x = df_X1.iloc[j*42:(j+1)*42, i].astype(np.float32)
    y = df_X1.iloc[j*42:(j+1)*42, i+1].astype(np.float32)
    plt.scatter(x, y, label=a_city)
  if i==1:
    plt.xlabel('Ave. of Temp in Aug.')
    plt.ylabel('Ave. of Max Temp. in Aug')
  elif i==2:
    plt.xlabel('Ave. of Max Temp. in Aug')
    plt.ylabel('Ave. of Min Temp. in Aug')
  else:
    plt.xlabel('Ave. of Min Temp. in Aug')
    plt.ylabel('Count of over 25 deg in Aug')
  plt.legend()
  plt.show()

4つ目のセルの実行結果のグラフ3つは以下の通り．

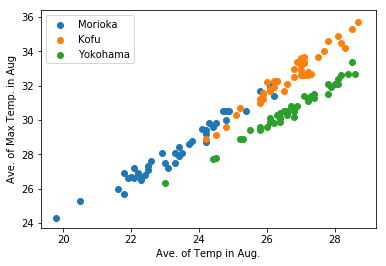
X軸が「8月の平均気温」，Y軸が「8月の日最高気温の平均」

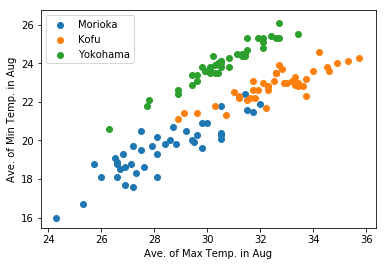
X軸が「8月の日最高気温の平均」，Y軸が「8月の日最低気温の平均」

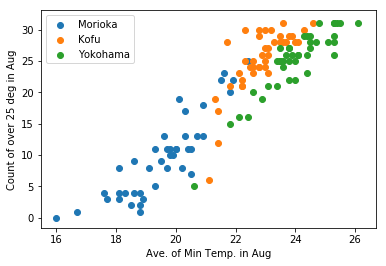
X軸が「8月の日最低気温の平均」，Y軸が「25度を超えた日数」

今は都市ごとに色分けをしているため判別しやすいが，横浜はどのグラフでも分離して見える（線形判別分析が簡単にできそう，すなわち判別の「直線」を引くことが可能に見える，「線形分離可能」と呼ぶ．）のに対して，盛岡と甲府はかなり被っているように見える．（盛岡と甲府は同じ直線上に載っているように見える）

主成分分析は「このグラフが分離して見えるような表示になるような「合成変数」を作成すること」が目的である．合成変数は任意の数（次元）で作成することができる．合成変数を2つ（2次元）にしてしまえば，2次元グラフでも簡単に表示できるようになるはず．

5つ目のセルでは，主成分分析を行い，グラフを描画している．scikit-learnに簡易的な主成分分析キットがあるので，これを利用する．

説明変数間で単位が違う場合「標準化」or「正規化」という作業をしなければならない（値のスケールをうまい具合に整えてくれるイメージ）．これは同じくscikit-learnの中に含まれているStandardScalerクラスで簡単に行うことができる．標準化するのは同じく説明変数のみであることに注意．

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 標準化する
scaler = StandardScaler()
df_X2 = scaler.fit_transform(df_X1.iloc[:, 1:])

# 合成変数を2次元で作る
pca_model = PCA(n_components=2)
pca_model.fit(df_X2)
# 変換行列ができたので，多次元の説明変数を2次元の合成変数に変換する
transformed_variables = pca_model.transform(df_X1.iloc[:, 1:])
# 使いやすいようにデータフレーム化しておく
transformed_df = pd.DataFrame(transformed_variables)
# 合成変数2つの散布図を描く
for i, a_city in enumerate(choosed_cities):
  plt.scatter(transformed_df.iloc[i*42:(i+1)*42, 0], transformed_df.iloc[i*42:(i+1)*42, 1], label=a_city)
plt.xlabel('Principal Component 0')
plt.ylabel('Principal Component 1')
plt.legend()
plt.show()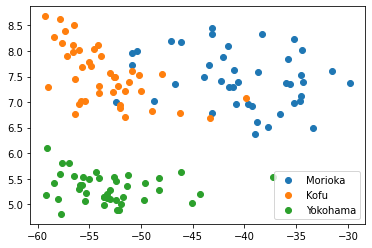

5つ目のセルで描画したグラフは以下の通り．

このグラフでは，X軸が主成分つまり合成変数0(Principal Component)0 , Y軸が主成分つまり合成変数1である．

合成変数では，盛岡，甲府，横浜が綺麗に分離しており，線形判別分析が容易になっている．この3都市の8月の気温に関しては，主成分分析 - 合成変数が有効であることを示している．

この状態で最初の目的である「4つの観測値から『都市の気候』をうまく表現したい．うまく説明できるようにしたい．」を達成できたかを考えると，「直線の補助線を引くことで，「この線のこちら側が盛岡で，この線のこちら側が甲府で，この線のこちら側が横浜です」とうように明確に説明できるようになる」ので，目的を達成したと言える．

寄与率

主成分分析でもう一つ確認しなければならないのが「寄与率」である．主成分分析をした後に，モデルを保持している変数のexplained_variance_ratio_という変数の中に寄与率が入っている．

# 寄与率の表示
print(pca_model.explained_variance_ratio_)

寄与率の出力結果は以下の通り．

[0.97995861 0.01258219]

寄与率というのは，それぞれの主成分つまり合成変数が「データをどれだけ表現できているか」を表したものである．寄与率の合計が1.0に十分に近ければ，合成変数のみでデータを十分表現できていると言っても良い．

寄与率の出力は配列になっており，0番目が主成分合成変数0の寄与率，1番目が主成分合成変数1の寄与率である．合計が1に十分に近いので，この2次元だけで元データを十分に表現していると言って良い．つまり「4次元あった変数は2次元に落とし込むことが可能」ということである．

逆に合計寄与率が低かった場合，「この次元数では元のデータを表現できているとは言い難い」となる．この場合，合成変数の次元数を増やす必要がある．1次元ずつ増やしていって，寄与率が1に十分近くなる次元数を探す．次元数を増やしても合計寄与率が上がらなくなった場合はそこで止める．

主成分分析の合成変数間の相関係数

# 合成変数間の相関係数の表示
print(transformed_df.corr())

「合成変数間の相関係数」は，普通にデータフレームの内部の相関係数を出力すれば良い．

              0             1
0  1.000000e+00 -1.182588e-15
1 -1.182588e-15  1.000000e+00

合成変数間の相関係数は非常に小さい（ほぼ0）．というのも，主成分分析の内部計算は「合成変数間の相関係数を低くする」ように調整するからである．逆に言えば「相関が高いものをまとめる」という調整とも言える．