本項でもGoogle Colaboratoryを使用する.(もちろんファイル読み込みの部分以外はJupyter Notebookでもよいし,一気にPythonのソースコードをまとめて書いて実行しても問題はない)
今回も,前回と同じ気象庁オープンデータを使用するが,取ってくるデータは違う.
線形単純回帰分析
xとyの関係が例えば「y = ax + b」という「線形」の「モデル」すなわち一次関数の直線で表現できると仮定し,実際に観測されたデータを用いて,その直線を表現するaとbを求めることを,線形回帰分析という.(xを説明変数(Explanatory Variable)もしくは独立変数,yを目的変数(Response Variable)もしくは従属変数,応答変数などと呼ぶ)
実際には「y = ax1 + bx2 + cx3 + dx4 + e」というモデルも考えられる.これは説明変数が4つ,目的変数が1つの場合である.(この説明変数の数は,「説明変数の次元」とも呼ぶ)
説明変数が1つの時「単純回帰分析」と呼び,説明変数が2以上の場合は「重回帰分析」と呼ぶ.とりあえず本項では「単純回帰分析」,特に「y = ax + b」のモデルで捉える単純線形回帰分析を扱う.
(なぜ「特に」かというと,「y = ax^2 + b」というモデルも,求めるべき係数aが説明変数「x二乗」に対して線形であることから,こういうモデルも「単純線形回帰分析」と呼べる,という理由による.この場合は「x二乗」をそのまま説明変数として使うため,計算上そのまま扱えるように説明変数の配列をを二乗になっている状態で作成しておく.)
最小二乗法
現実に観測されたデータには「ノイズ」が乗っている.すなわちどんなデータも綺麗なy = ax + bの直線上にあることは殆どなく(統計学的にはありえないと仮定する),そこからズレていることが前提である.そこで観測された全てのデータの,直線で表されるyの量との「ズレ」の総量を最小にする「最小二乗法」が一般的に用いられる.
Scikit-LearnというPythonのライブラリは,回帰分析などの機械学習アルゴリズムを豊富に備えており,簡単に学習ができるようになっている.目的変数と説明変数の観測値のデータを表で作り,それをfit(説明変数, 目的変数)とすることで,簡単にこのような機械学習を実行することができる.
そのためにはpandasのDataFrameという形式でCSVなどの表データを扱うと都合が良い.
ちなみに単純回帰分析の英語名は「Ordinary Least Squares」であり略称がOLSである.
対象データ
気象庁のオープンデータサイトより,今回は,東京都八王子市の1977年〜2018年の8月の月平均気温,日の最高気温の月平均,日の最低気温の月平均,3つが入っているデータをダウンロードした.八王子市でも夏の温暖化が進んでいるとすれば,説明変数xを年(データがある1977年〜2016年を0〜にする),応答変数yを日中最高気温の月平均として,単純線形回帰分析をかけると「y = ax + b」が成立するかもしれない.
気象庁からダウンロードしたCSVはこんな感じである.
scikit-learnを使った回帰分析のコード例
最初のセル
from google.colab import files
uploaded = files.upload()これを実行すると,ファイルを読み込んでくれるようになるので「ファイルを選択」してアップロードすると,以下のようにGoogle Colaboratory内に読み込まれる.

2つ目のセル
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
df = pd.read_csv('hachioji-temp-data.csv', encoding='SHIFT-JIS', header=2)
# PandasのDataFrameという形式で読み込まれる
# 文字コードはSHIFT-JIS, 官公庁のオープンデータや,歴史が古い企業のデータはエクセルから書き出すものが多いからか,SHIFT-JISが多い.
# このheader=2は頭から2行分は不要な情報なので読み飛ばす,という意味
df.head()
# チェック用として,頭の部分だけ表示
# DataFrameでは,この状態で一番上の行が「列の名前」として認識され,操作することができる.
# 列の名前になっているので,この行を行番号では操作できなくなる.実行すると,CSVが読み込まれる
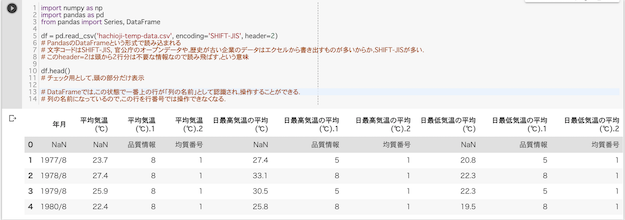
3つ目のセル.余計なものが1行入ってたので削除.
# 列の名前が入っている行の下に余計なものが一つあったので(行番号0になる),削除
df = df.drop(0) #0番目の行を削除する
df.head()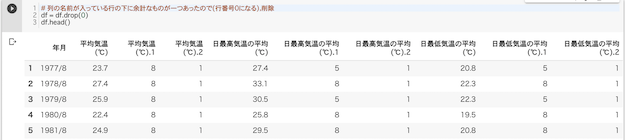
4つ目のセル.
# 「日最高気温の平均(℃)」列のみを抽出
# 1次元目の「:」は行のインデックスが「0~あるだけ」
# つまり全ての行で,このラベルがついた列を抽出,という意味になる
df = df.loc[:, ['日最高気温の平均(℃)']]
df.head()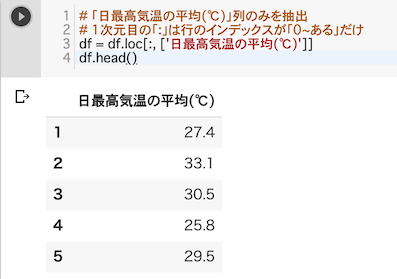
5つ目のセル.データの形状を読み込めるように加工する.
今回は1977年〜2918年のデータなので説明変数である「年」と目的変数である「月間の最高気温の平均」は42個(42年分)ある.したがって,ここで説明変数と目的変数に与える「配列の形状」が(42, 1)になっている必要がある.この「形状」は,DataFrameクラスのインスタンスの中のshapeという変数に格納されている.
matplotlib.pyplotというライブラリを使って,その加工した説明変数と目的変数をプロットしてみる
# 説明変数は,その西暦年年にする
# 今は説明変数が「西暦年」1つなので,西暦年1次元のNumpy配列(1977~2018)を作る.
# np.arange(a, b)は,aからb-1までの整数のNumpy配列を作る関数
# 重回帰分析をするためには,複数の説明変数が必要となるので,2次元配列を取ることになる.
# そこでreshape(42, 1)を使って,無理やり2次元のNumpy配列にして格納する.
X = np.arange(1977, 2019).reshape(42, 1)
# 目的変数を 「日最高気温の平均(℃)」にする
# Nanが入っていることがあるので,Nanが入っていたらその行を取り除くコード
# 入っていないこともある
# 入っていたら当然行が減ってズレるので,
# 説明変数Xの西暦の方も適切にその行を取り除く必要がある.
y_temp = np.logical_not(pd.isnull(df))
mask = np.logical_and(np.cumsum(y_temp)!=0, np.cumsum(y_temp[::-1])[::-1]!=0)
df = df.loc[mask['日最高気温の平均(℃)'].tolist()]
# 目的変数は「1つ」なので,必ず1列になるので,「データは1次元」,「全体として2次元」であることを確認する
# DataFrameのvaluesという変数には,Numpyの2次元配列が入っているので,これを用いる
Y = df.values
# 説明変数と目的変数の行列の形状を確認する
#(現在は説明変数一つなので,同じになっている必要がある)
print('説明変数Xの形状', X.shape) #(サンプル数, 説明変数の数(今は1))になっている必要がある
print('説明変数Yの形状', Y.shape) #目的変数なので, (サンプル数, 1)になっている必要がある
#一度グラフに表示してみる
import matplotlib.pyplot as plt
plt.plot(X, Y)
plt.show()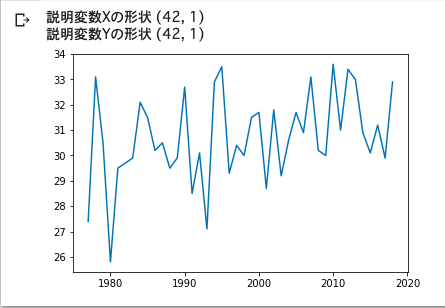
6つ目のセル.いよいよ学習して,結果を同じく表示する.
学習した後は,そのインスタンスのpredict()関数に,説明変数を突っ込めば,予測した値が出てくるので,そちらを観測値の後にプロットしている.
import scipy
import sklearn
from sklearn import linear_model
# 回帰分析するクラスのインスタンスを作る
ols_model = linear_model.LinearRegression()
# 回帰分析を走らせる(学習する)
ols_model.fit(X, Y)
# 結果を出力していく
# 回帰係数(傾き)
print('回帰係数(傾き):', ols_model.coef_)
# 切片 (誤差)
print('切片:', ols_model.intercept_)
# 決定係数
print('決定係数', ols_model.score(X, Y))
# データにどのぐらいフィットしているかを表す値
# グラフを表示
# まず観測値を再度プロットする
plt.plot(X, Y)
# 次に回帰分析した結果をプロットする
# 回帰分析インスタンスのpredict関数に説明変数Xを入れると,予測した目的変数を出してくれる
predictedY = ols_model.predict(X)
# それを表示
plt.plot(X, predictedY)
# 表示
plt.show()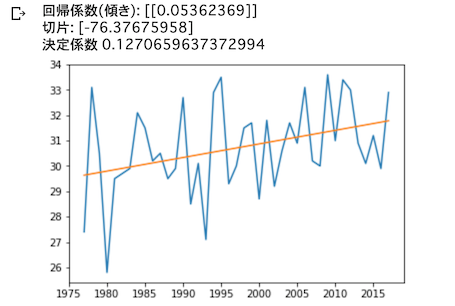
式の結果は「y = 0.05362 x + (-76.3767)」であった.プロットしてみると,なんとなく合っているような気がする.
(切片が大きくマイナス?と考えたかもしれないが,説明変数が1977からスタートしていることに注目.この切片は0の時,つまり西暦0年の時の8月の気温に相当する.実際にそんなことはないと思うので,産業革命以降に気温の上昇が始まった,つまり産業革命以降の実際の記録から回帰分析すれば,もっと傾きが大きくなる,と考えるのが妥当だろう)
決定係数とは「予測がどれだけ観測データにフィットしているか」を表す値である. 今回のデータは気温であり,気温の変動は周期性があり毎年の変動が多いので,今回は決定係数は低くても,全体的にみてこの傾きが観測データになんとなく沿っていることがわかれば十分である.
statsmodelsを使った回帰分析のコード例
scikit-learnは機械学習のライブラリなので,結果は「なんとなく合っているような気がする」だったが,高機能な統計用のライブラリは「統計的な正当性」(例えば検定など)も同時に行ってくれるため,論文のデータなどに使う場合は,そちらを用いると都合が良い.
例えば,分析機能に特化しているライブラリstatsmodelsは,検定結果まで出してくれる.
先ほどの6番目のセルを以下に置き換える.
statmodelsでの回帰分析のコードの書き方は,scikit-learnを使った場合とほぼ同じだが,学習済みのols_modelでpredictするのではなく,ols_resultという変数を用意してfitした結果を格納し,ols_result.predict()していることに注意.
import statsmodels.api as sm
nsamples = Y.shape[0]
ols_model = sm.OLS(Y, sm.add_constant(X))
ols_result = ols_model.fit()
print(ols_result.summary())
predictedY = ols_result.predict(sm.add_constant(X))
plt.plot(X, Y)
plt.plot(X, predictedY)
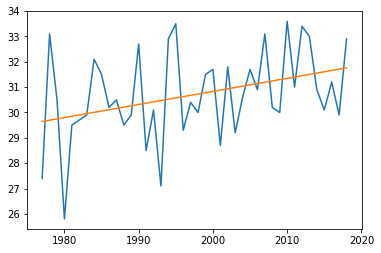
plt.show()結果は以下の通り
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.126
Model: OLS Adj. R-squared: 0.105
Method: Least Squares F-statistic: 5.789
Date: Wed, 21 Aug 2019 Prob (F-statistic): 0.0208
Time: 11:01:05 Log-Likelihood: -80.482
No. Observations: 42 AIC: 165.0
Df Residuals: 40 BIC: 168.4
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -72.3855 42.846 -1.689 0.099 -158.980 14.209
x1 0.0516 0.021 2.406 0.021 0.008 0.095
==============================================================================
Omnibus: 0.065 Durbin-Watson: 2.291
Prob(Omnibus): 0.968 Jarque-Bera (JB): 0.183
Skew: -0.085 Prob(JB): 0.913
Kurtosis: 2.725 Cond. No. 3.29e+05
==============================================================================
求める式 y = ax + bの,a(係数: 結果のx1)と,b(切片: 結果のcost)に,それぞれp値(P>|t|)が出ているが,これはt検定などでいうところのp値である.特に回帰係数aに対応する帰無仮説と対立仮説は,それぞれ以下のようになる.
- 帰無仮説: x1つまり説明変数は,目的変数に影響を与えない.
- 対立仮説: x1説明変数は,目的変数に影響を与える変数である.
という風になる.すなわちこのp値が0.05を超えている場合は,帰無仮説が棄却されず「なんか回答が得られたけど,実際のところ,この変数は影響与えてないよねー」という意味になる.
今回は明確に傾きが影響していることがわかっているのでp値は低いが,説明変数が複数である重回帰分析ではこのp値を見ながら説明変数のセットを探していくことになる.
statsmodels で線形回帰 - Qiitaというページでは,二次関数を線形回帰分析で解くための「線形基底関数モデル」に関する説明もある.