こーひーをぶんなぐれ！ - Rのベクトルと行列

Rのベクトルと行列(matrix)

前項でも，配列としてのベクトル，2次元配列としての行列はやったが，本項ではベクトルとしてのベクトル，行列としての行列について行う．

Rは数学計算向けなので，Pythonに比べコンピュータ的な考え方ではなく数学的な考え方で書く．

ベクトルや行列は，中のデータ型（整数，実数，文字列）が揃っていなければならない．

Vector

前項では，array関数に次元dimとその要素数を指定して配列の生成を行なっていたが，

 # 1次元4要素の配列
vec1 <- array(c(2, 4, 6, 8), dim=c(4))

実はc関数だけでも，同じことができる．

# c関数に要素を指定して生成
vec1 <- c(2, 4, 6, 8) 
vec2 <- c(1, 2, 1, 2)

各要素の演算

# ベクトルの各要素に2をかける
print(vec1 * 2)

[1]  4  8 12 16

# vec1の各要素からvec2の各要素で引く
print(vec1 - vec2)

[1] 1 2 5 6

要素の引き算は当然要素数（ベクトルの次元数）が合っていないとできない．

ベクトルの演算

# ベクトル同士の積(内積)
print(vec1 %*% vec2)

     [,1]
[1,]   32

# ベクトル同士の直積
print(vec1 %o% vec2)

     [,1] [,2] [,3] [,4]
[1,]    2    4    2    4
[2,]    4    8    4    8
[3,]    6   12    6   12
[4,]    8   16    8   16

要素を規則的に生成

# sequence関数で生成
vec3 <- seq(1:5) # c(seq(開始:終了))
print(vec3)

[1] 1 2 3 4 5

vec3 <- seq(1, 10, length=5) # ,であることに注意．1から10まで要素数5の等差数列，つまり5段階で
print(vec3)

[1]  1.00  3.25  5.50  7.75 10.00

vec4 <- seq(1, 10, by=2) # ,であることに注意．1から10まで，2ずつ増やしながら．
print(vec4)

[1] 1 3 5 7 9

# repeat関数で生成
vec5 <- rep(1:2, times=5) # rep(繰り返し開始値:繰り返し終了値, time=繰り返し回数)
print(vec5)

[1] 1 2 1 2 1 2 1 2 1 2

vec6 <- rep(1:2, length=5) # rep(繰り返し開始値:繰り返し終了値, length=要素数) 要素数に達するまで繰り返される
print(vec6)

[1] 1 2 1 2 1

ベクトルの要素へのアクセス

# 要素へのアクセス
print(vec1[3]) #インデックスが1~であることに注意

[1] 6

# 要素の追加
# 非破壊であることに注目
vec7 <- append(vec1, 9)
print(vec7)

[1] 2 4 6 8 9

ランダムで生成したベクトル

確率関数

Rでは確率関数を使う．分布などにも使えるが，乱数配列を生成するには頭文字にrを使う．

r確率関数名というのが乱数生成の基本．例えば一様乱数なら，runif関数(random uniform)になるし，正規分布に従う関数なら，rnorm関数(random normal distribution)になる．

# -1から1までの一様分布を10個生成してベクトルに格納 runifはrandom uniformの略
p1vec <- runif(10, min=-1.0, max=1.0)
print(p1vec)

 [1] -0.59493549 -0.53270312  0.93013569  0.52710300 -0.03046344  0.79123780
 [7] -0.34240593 -0.78756932  0.01953284 -0.39418644

hist(p1vec) # ヒストグラムを描く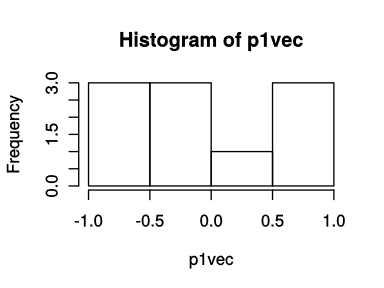

# 平均5，標準偏差2の分布に従う乱数を10個生成してベクトルに格納
p2vec <- rnorm(100, mean=5, sd=2) 
hist(p2vec)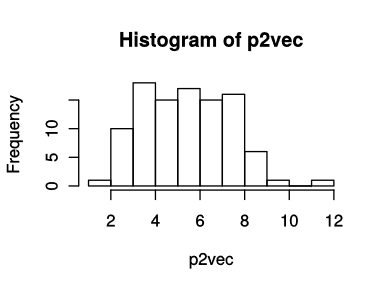

要素の集計ビルトイン関数

配列の要素の集計のビルトイン関数が充実している．

# 要素の集計ビルトイン関数
print(sum(p2vec)) # 合計

[1] 541.4379

print(mean(p2vec)) # 平均

[1] 5.414379

print(median(p2vec)) # 中央値

[1] 5.54973

print(max(p2vec)) # 最大値

[1] 11.31937

print(min(p2vec)) # 最小値

[1] 1.530532

print(which.max(p2vec)) # 最大値のインデックス

[1] 38

print(which.min(p2vec)) # 最小値のインデックス

[1] 44

summary(p2vec) # 全部表示

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.531   3.868   5.550   5.414   6.841  11.319 

print(unique(vec5)) # 重複する値を削除した配列を返す

[1] 1 2

行列

2次元配列というより「行列」である．前項の通り，array関数に次元dimを与えても作ることができるが，

mat1 <- array(seq(1, 9), dim=c(3, 3)) # 2次元で，3要素, 3要素の配列
print(mat1)

matrix関数を使ったほうが便利．

# 要素を指定して生成
mat1 <- matrix(c(1, 2, 3, 4), nrow=2, ncol=2)　# 2*2の行列

# さらに簡単に, nrowとncolは省略できる
mat1 <- matrix(c(1, 2, 3, 4), 2, 2) 
print(mat1)

     [,1] [,2]
[1,]    1    3
[2,]    2    4

# sequence関数で生成
mat2 <- matrix(c(seq(1:9)), 3, 3) # 3 * 3の行列
print(mat2)

     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

# zero行列
mat3 <- matrix(0, 3, 3) # 3*3のゼロ行列
print(mat3)

     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    0
[3,]    0    0    0

単位行列を作るのは，matrix関数ではなくdiag関数を使う．

# 単位行列
mat4 <- diag(3) # 3*3の単位行列
print(mat4)

     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

行列とベクトルの掛け算

ベクトルは一度行列に変換してから，行列同士の掛け算として，行う．

# 行列とベクトルの掛け算
# ベクトルは一度行列に変換してから，行列同士の掛け算として，行う．
vec8 <- c(1:3)
print(vec8)
vec9 <- matrix(vec8, nrow=3, ncol=1) # 3行1列の行列に変換
print(vec9)
mat5 <- mat2 %*% vec8 # 掛け算
print(mat5)

[1] 1 2 3
     [,1]
[1,]    1
[2,]    2
[3,]    3
     [,1]
[1,]   30
[2,]   36
[3,]   42

vec10 <- matrix(c(1:3), nrow=1, ncol=3) # 1行３列の行列に変換
print(vec10)
mat6 <- vec10 %*% mat2 # 掛け算
print(mat6)

     [,1] [,2] [,3]
[1,]    1    2    3
     [,1] [,2] [,3]
[1,]   14   32   50