こーひーをぶんなぐれ！ - CSVデータからの分散分析と多重比較

t検定の項と同じく，気象庁のオープンデータから，1977年〜2018年の，江戸川臨海，東京，青梅，八王子，練馬，府中の5箇所の，1月の月平均気温データと，8月の月平均気温データを用いる．

前回とは異なるデータ形式にする必要があるので，Googleスプレッドシートをコピーしておくこと．

異なる2地点以上の比較

前回のt検定は，2つの群の間で，統計的に本当に違いがあるかをいうためのものだった．，

今回は，1977年〜2018年の，青梅，八王子，府中の3箇所，つまり3群で違いがあるかを見る．

分散分析(一元配置分散分析)とは

今回の場合は「3つ以上の地点の気温データ群の間の差を，統計的に（ある程度）保証してくれる」のが分散分析である．要するに3群以上の検定．

分散分析にもt検定と同じく，対応がある場合と対応がない場合があるので，前回を復習しておくこと．今回は対応がない場合のみを取り扱う．

分散が等しいかどうかをみる時（t検定でいうF検定に相当）と，分散分析をする時では，食わせるデータの形が違っていることに注意．Rで多く使われている分散分析のパッケージ（aov関数）を使うには，データが「スタック形式」になっている必要がある．

Bartlett検定

t検定では，2群の分散（散らばり方）が等しい時とそうでない時で，適用する方法が違っていた．（Studentのt検定と，Welchのt検定）3群以上の場合に等分散性をみるのがBartlett検定である．

F検定と同じく，帰無仮説は「与えられた3群（以上）の分散は等質である」，対立仮説は「与えられた3群（以上）の分散は等質であるとは言えない」である．したがって結果のp値の見方も同じく，0.05以上であれば帰無仮説が棄却されず「分散が等質である」となる．

bartlett.test関数を用いるが，分散分析と同じく，データが「スタック形式」になっている必要がある．

データの形式：アンスタック形式とスタック形式

Rの標準の分散分析およびBartlett検定は，t検定とは異なり「値とラベルがペアになったものがたくさんある」というデータ形式で与えなければならない．ここでいう「ラベル」とは，この値がどの群のものなのか，を表す．

気温の配列は全部繋げた上で，観測地点ラベルの配列も作り，それを2次元配列にまとめる．その後次元を変更し 「気温と観測地点ラベルが対応したペアが，126個存在する」という感じに変更する．

このような，値とラベルが順不同で積み重なっているデータ形式を「スタック形式」という．それに対して先に作った表のデータは「アンスタック形式」と言う．表にするとわかりやすい．

アンスタック形式のデータのイメージ

江戸川	青梅	八王子
3.1	0.7	0.9
5.4	2.6	2.9

スタック形式のデータのイメージ

気温	地点ラベル
3.1	江戸川
0.7	青梅
0.9	八王子
5.4	江戸川
2.6	青梅
2.9	八王子

データの作成

Googleスプレッドシートで「スタック形式」のデータを作成する．

1月のCSVファイルを読み込んだ状態．CSVファイルはt検定で使ったものと同一である．

スプレッドシート本体のファイル名を変更しておく．

シートの名前も変更しておく．

t検定の時と同じように，不要な行列を削除する．

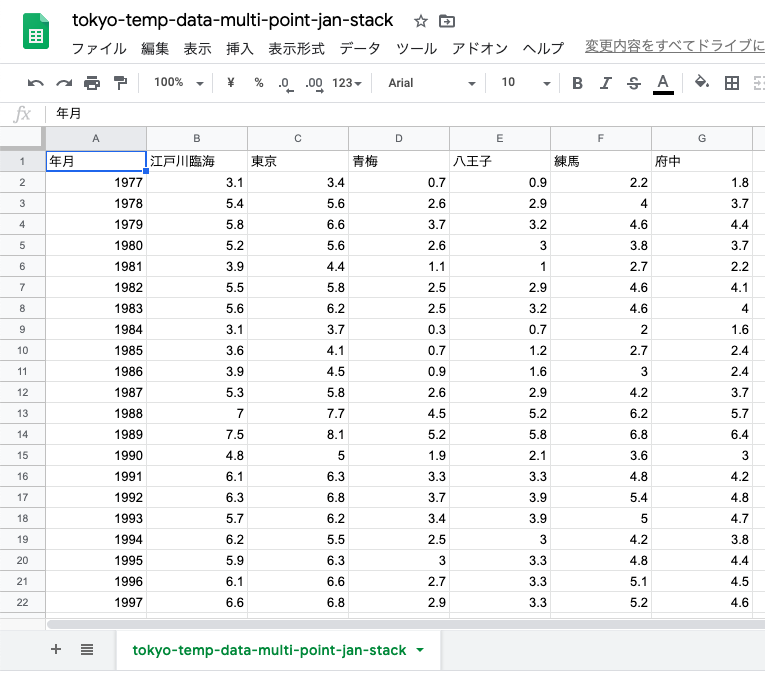
今回は，青梅，八王子，府中の3箇所を比較するので，それ以外の列は削除．

青梅，八王子，府中だけが残った状態．これは「アンスタック形式」．

一番上に行を挿入．ここに新しい列名を入れる．

「値」の列名として「平均気温」，地点ラベルの列名は「群」にする．

八王子の1977年〜2018年を「切り取り」

青梅の下（2018年の下）に「貼り付け」

青梅と八王子の平均気温が1列に「スタック」（積み重ね）された．

同じく府中のデータも切り取って，

八王子のデータの下に貼り付け．

青梅と八王子と府中の平均気温が1列に「スタック」された．

「青梅」というセルを「コピー」して，

青梅の値が入っている一つ右，つまり1977年〜2018年の一つ右のセルを選択して，「貼り付け」

青梅の値である「平均気温」と，群ラベルである「地点」がセットになった．

同じように，八王子と府中の群ラベルもコピーして，群ラベルを完成させる．

元々の列名があった行，つまり「青梅」だけが入っている3行を削除．

同じように「八王子」だけが入っていた元々の列名があった行を削除．

府中も削除

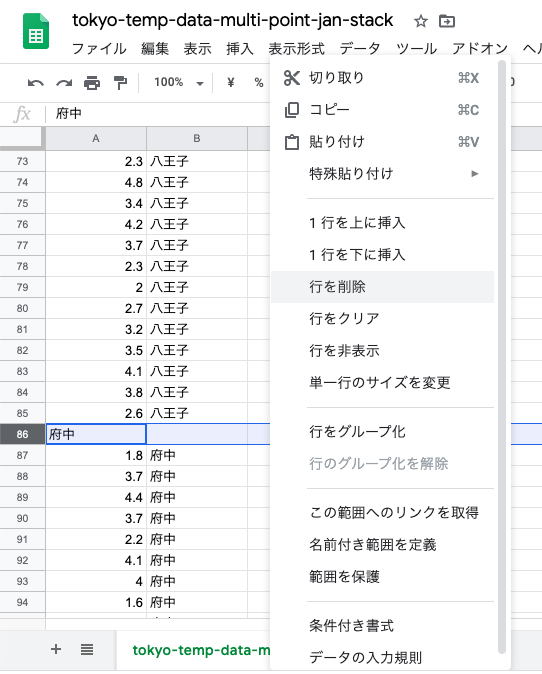
そうしたら，同じようにCSV形式で「Webに公開」しておく．

url <- '公開したURL'
df <- read.csv(url, header=TRUE)  #　header=TRUE　は第１行が列の変数名
# 欠損値のある行を削除
df <- na.omit(df)
head(df)

Rで読み込み，頭数行を表示．

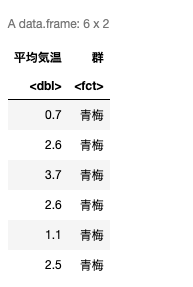
ちゃんとできているか，一応printしてスクロールしながら全部チェックする．

print(df)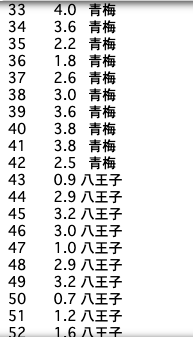

Bartlett検定

# Barlett検定
bartlett.test(formula=df$'平均気温'~df$'群')

Bartlett検定を実行する．formulaオプションに与えるのは， 目的変数のベクトル~説明変数のベクトルという形式．（なんとなく想像がつくと思うが，実は線形分析をやっている）

Bartlett検定の帰無仮説は「分散は等質である」，対立仮説は「分散は等質とは言えない」．

Bartlett検定の結果は以下の通り．

	Bartlett test of homogeneity of variances

data:  df$平均気温 by df$群
Bartlett's K-squared = 0.0092943, df = 2, p-value = 0.9954

p値が，0.99と高く，0.05を大きく上回っているので，帰無仮説は棄却されず「3つの地点の1月の平均気温の分散は等質である」ということになる．

分散分析

bartlett検定と同じように，formulaオプションをつけて列名を入れ，aov関数を呼び出すと，それだけで分散分析ができる．aov関数の結果をみるときには変数に代入し，summary関数で表示することに注意．

result_aov <- aov(formula=df$'平均気温'~df$'群')
summary(result_aov)

結果表示は以下の通りになる．

             Df Sum Sq Mean Sq F value   Pr(>F)    
df$群         2   39.0  19.502   15.76 8.07e-07 ***
Residuals   123  152.2   1.238                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Pr(>F)の項目がp値である．結果は8.07e-07なので，十分に小さく，帰無仮説「3つの地点の1月の平均気温には差がない」が棄却された，つまり「3つの地点での1月の平均気温には差がある」と言うことができる．

その行の下は，***の数で何％水準で優位さがあると言えるかを表しており，1行目に***とアスタリスクが3つついていることから，今回の3地点に関して，ほぼ確実に「統計的に違う」と言って良い．

多重検定

この「有意差が出た」時点で平均だけを見て「全部の地点で差がある！」といってしまいがちだが，そうではなく「どこか1つ以上の地点で差がある」だけである．

分散分析自体は，どの群とどの群に差があるのかを出してくれないため，それを見つけるために多重検定というのを行う．

全ての地点を「クロス」で検定するみたいな言葉のイメージで，一番簡単なのが「分布の調整による多重比較法であるTukey-Kramerの多重検定」と呼ばれる手法である．

「Tukey-Kramerの多重検定」は，「各群の母分散も等しい(分散の等質性)」時につかえる．各群のサイズが等しくなくてもよい（この場合だと全ての地点が42個で同じサイズだが）．

「各群の母分散も等しい」とは，簡単に言えば「全ての地点の気温データのばらつきの形が，だいたい同じ」と思っておくと良い（これは統計的にも確かめることができる．母分散の定義は「母集団の特徴を表す母数」参考: 母分散と不偏分散)

ちなみに名前の似ている「Tukeyの方法」という多重検定方法もあるが，これは各群のサイズが同じである必要がある．(R で標準で使えるTukeyHSD関数はTukey-Kramerなので，群サイズを気にせず使える．TukeyHSDの「HSD」は，Honestly Significant Differenceの略で，Tukey-Kramerの別名）

実行は以下のようにする．

TukeyHSD(result_aov)

Tukey-Kramerの関数TukeyHSDは，aov関数の「結果を使う」ことに注意．（先ほどaov関数の結果を変数に代入し，summary関数で表示したのはこのため）

tukey-Kramerの結果は以下のようになる．

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = df$平均気温 ~ df$群)

$`df$群`
                  diff        lwr        upr     p adj
府中-八王子  1.0095238  0.4336054  1.5854422 0.0001752
青梅-八王子 -0.2880952 -0.8640137  0.2878232 0.4632930
青梅-府中   -1.2976190 -1.8735375 -0.7217006 0.0000013

一番右のp adjという列名になっている列がp値（正確には調整p値）である．

この結果を見ると，青梅-八王子間のみが，0.05を上回っている．

すなわち，青梅-八王子間は「同じ」という帰無仮説が棄却されなかったことになり，逆に府中-八王子間，府中-青梅間では棄却されていることから「1977年から2018年までの1月平均気温では，この3地点のみでは府中だけが有意に気温が高い」ということができる．

分散分析と多重比較

「多重比較の方でも有意差を出してくれるなら，多重比較だけやればいいのではないか？」という疑問が出てくる．

「分散分析では有意差が出なかったが，Tukey-Krammerの多重比較では有意差が出た」なんてこともありうるし，その逆，つまり「分散分析で有意差が出たが，Tukeyの多重比較では有意差が出なかった」ということもありうる．特に群が増えてくるとTukeyの多重比較では「帰無仮説の数が増えて有意になりにくくなる」．

つまり，分散分析と多重比較は完全に別のものであり，従属関係にはない．「分散分析で有意差がある→多重比較を行う」ではなく，両方を独立させて目的に応じて適用を考える必要がある．

参考：分散分析の下位に多重検定を置くな

t検定を3回やってはダメな理由

多重比較を使わずに，最初からt検定を3回やればいいのでは？と思うかもしれないが，これはやってはいけない．

青梅，八王子，府中で，2群間の検定をそれぞれ「青梅-八王子間」「八王子-府中間」「府中-青梅間」でそれぞれ「有意水準5%で行う」とすると，「この組み合わせの少なくとも1つは有意差がある」となる確率の計算式は以下のようになる．

1 - (1 - 0.05) * (1 - 0.05) * (1 - 0.05)

つまり「0.05を基準に検定したつもりが実際には0.14で検定している」ことになってしまう．0.14の基準は0.05よりもはるかに甘いので「非常に甘く見ている」ということである．

これは当然「比較する群が増えれば増えるほど甘くなる」ということであるから，3群以上の場合は必ず分散分析と多重比較を行う．

二元配置分散分析

今回行なった一元配置分散分析は，前述の通りアンスタック形式の表で言えば以下のようになる．

青梅	八王子	府中
22.8	23.7	23.8
26.6	27.4	27.6
24.9	25.9	26.1
21.7	22.4	22.5

これに対し二元配置分散分析というものもあり，2つの要素の違いを見る．例えば観測地点の名称ではなく，観測時点でのその地点の天気で見ると，以下のようなデータを取り扱うことになる．（平均気温ではなく，その観測時の気温）

観測時の天気\観測地点	青梅	八王子	府中
晴れ	26.6	27.4	27.6
晴れ	26.6	27.4	27.6
雨	24.9	25.9	26.1
雨	21.7	22.4	22.5

これを分析する時には，以下の3点に注目することになる．

1. 地点によって気温に違いはあるのか
2. 天気によって気温に違いはあるのか
3. 地点と天気の2つの要素による相乗効果はあるのか

この3つ目の「相乗効果」を「交互作用」と呼び，交互作用を分析するのがわざわざ天気を入れた理由であり，これを分析することが二元配置分散分析となる．