今回も,前回と同じ気象庁オープンデータを使用するが,取ってくるデータは違う.
線形単純回帰分析
xとyの関係が例えば「y = ax + b」という「線形」の「モデル」すなわち一次関数の直線で表現できると仮定し,実際に観測されたデータを用いて,その直線を表現するaとbを求めることを,線形回帰分析という.(xを説明変数(Explanatory Variable)もしくは独立変数,yを目的変数(Response Variable)もしくは従属変数,応答変数などと呼ぶ)
実際には「y = ax1 + bx2 + cx3 + dx4 + e」というモデルも考えられる.これは説明変数が4つ,目的変数が1つの場合である.(この説明変数の数は,「説明変数の次元」とも呼ぶ)
説明変数が1つの時「単純回帰分析」と呼び,説明変数が2以上の場合は「重回帰分析」と呼ぶ.とりあえず本項では「単純回帰分析」,特に「y = ax + b」のモデルで捉える単純線形回帰分析を扱う.
(なぜ「特に」かというと,「y = ax^2 + b」というモデルも,求めるべき係数aが説明変数「x二乗」に対して線形であることから,こういうモデルも「単純線形回帰分析」と呼べる,という理由による.この場合は「x二乗」をそのまま説明変数として使うため,計算上そのまま扱えるように説明変数の配列をを二乗になっている状態で作成しておく.)
最小二乗法
現実に観測されたデータには「ノイズ」が乗っている.すなわちどんなデータも綺麗なy = ax + bの直線上にあることは殆どなく(統計学的にはありえないと仮定する),そこからズレていることが前提である.そこで観測された全てのデータの,直線で表されるyの量との「ズレ」の総量を最小にする「最小二乗法」が一般的に用いられる.
Rにはlsfitという関数やlmという関数があり,最小二乗法による線形回帰を行うことができる.lsfit関数は"This function is the "old" way to do linear regression in S and S-PLUS"と書かれているように,古く,インタフェースやデータの与え方に制限が多いため,現在はほとんどの教科書でlm関数を使用しているようだ.
lm関数の方は,data.frame形式で与えることができるため,都合が良い.
ちなみに単純回帰分析の英語名は「Ordinary Least Squares」であり略称がOLSである.
対象データ
気象庁のオープンデータサイトより,今回は,東京都八王子市の1977年〜2018年の8月の月平均気温,日の最高気温の月平均,日の最低気温の月平均,3つが入っているデータをダウンロードした.八王子市でも夏の温暖化が進んでいるとすれば,説明変数xを年(データがある1977年〜2016年を0〜にする),応答変数yを日中最高気温の月平均として,単純線形回帰分析をかけると「y = ax + b」が成立するかもしれない.
気象庁からダウンロードしたCSVはこんな感じである.
これを前項の通り,Google SpreadSheetに読み込ませる.
読み込んだ状態.
不要な行を削除していく.
不要な行を削除し終わった状態.
不要な列も削除していく.
不要な列を削除し終わった状態.
列名を,前項と同じく,以下のように整える.(Rの標準のdata.frameは列名が長いと受け付けてくれないための対処)
今回は年を「数字」として目的変数とする.列名を「年」にした.そこで年の列の「8月」の部分を取り除く.
年の列を空にしてから,1行目と2行目に年を入力して,範囲選択しておく.
範囲選択の右下の四角を「下にドラッグして引っ張る」と,転戦で枠が広がる.
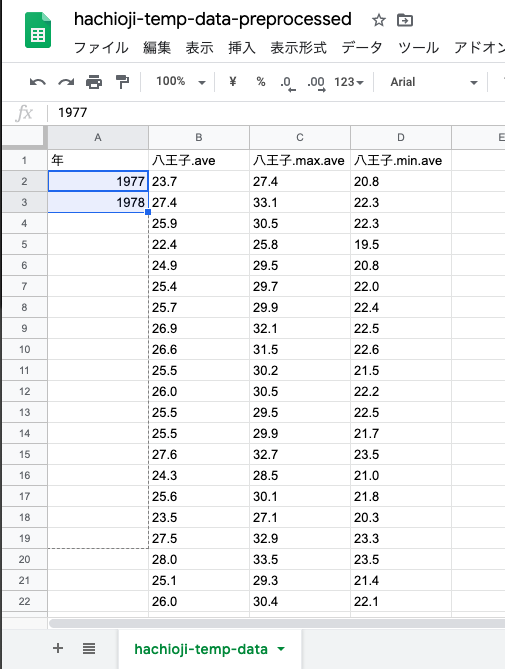
すると,勝手に「+1ずつされた並びの列ができる」
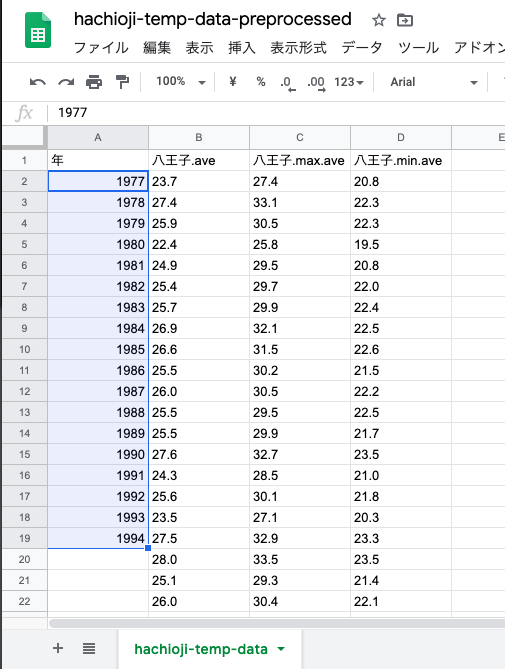
この状態で,前回のようにWebにCSV形式で公開し,URLを取得しておく.
8月の平均気温のグラフ表示
前回と同じように読み込み,最初の数行を表示.
url <- 'Google Spreadsheetで公開したCSVのURL'
df <- read.csv(url, header=TRUE)
head(df)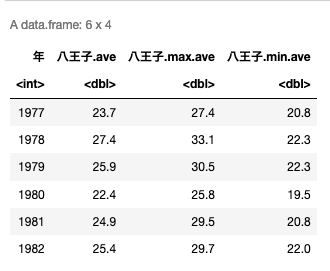
8月の平均気温の変化をグラフに表示してみる.X軸が「年」の列,Y軸が「八王子.ave」の列である.
plot(df$'年', df$'八王子.ave', type='l', xlab='year', ylab='Ave. of Aug. Temp.')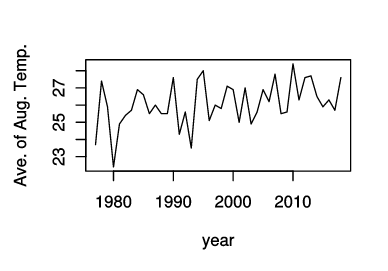
lm関数を使ったでの線形回帰分析
回帰分析を行うlm関数は以下のような書式になっている,とりあえず埋める必要があるのはformula,dataである.
lm(formula, data, subset, weights, na.action,
method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
singular.ok = TRUE, contrasts = NULL, offset = NULL, ...)
formulaには「式」を与える必要がある.今回は「y(8月の平均気温) = a * x(年) + b」を求めたい.formulaの式の数式の書き方は「 = 」を「 ~ 」で置き換える.さらに求めるaやbは省略する.したがって「y = ax + b」は
y ~ xと書く.
さらに目的変数yや説明変数xには,data.frameの「列名」が使える.すなわちformula部分に与えるのは,
八王子.ave ~ 年と書くことになる.
dataには普通に,先ほどCSVを読み込んだdata.frameを与えれば良い.
result.lm <- lm(formula="八王子.ave ~ 年", data=df) # 結果はオブジェクトで返ってくるので,変数で受ける
summary(result.lm) # 結果をsummary関数で表示で,回帰分析を実行し,その結果を見ることができる.結果は以下の通り.
Call:
lm(formula = "八王子.ave ~ 年", data = df)
Residuals:
Min 1Q Median 3Q Max
-2.9705 -0.8503 -0.1538 0.8859 2.1104
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -54.73755 30.24651 -1.810 0.0779 .
年 0.04046 0.01514 2.672 0.0109 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.189 on 40 degrees of freedom
Multiple R-squared: 0.1515, Adjusted R-squared: 0.1302
F-statistic: 7.139 on 1 and 40 DF, p-value: 0.01086Estimateが求めた,a(傾き),b(欠片)であり,「(Intercept)」が欠片,つまりここではb,「年」が傾き,つまりここではaとなる.
つまりこの結果は,y(8月の平均気温) = 0.04046 * x(年) - 54.73755であると言っている.
この式で表される直線を,平均気温の推移のグラフに重ねてみよう.
y = ax + bの直線を引くには,abline関数を使う.引数はaとbが逆になっていることに注意.
# y = ax + bの直線を引くには,abline関数を使う
plot(df$'年', df$'八王子.ave', type='l', xlab='year', ylab='Ave. of Aug. Temp.')
par(new=TRUE)
# abline関数は abline(b, a)で使う
abline(-54.73755, 0.04046)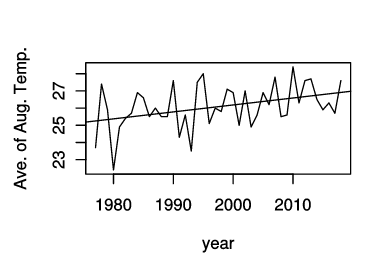
なんとなく合っているような気がする.
また,lm関数が出力したオブジェクトを,この関数を計算するpredict関数に食わせることで,説明変数xから説明変数yを出力することができる.したがってabline関数を使わずに,以下のような書き方もできる.
plot(df$'年', df$'八王子.ave', type='l', xlab='year', ylab='Ave. of Aug. Temp.', xlim=c(1977,2018), ylim=c(20, 30))
par(new=TRUE)
predict.aug.ave.temp <- predict(result.lm)
plot(df$'年', predict.aug.ave.temp, type='l', xlab='', ylab='', xlim=c(1977,2018), ylim=c(20, 30))predict関数はその名前の通り「予測をする」関数なので,説明変数に新しい値を入れたれば,それに対応した値を出してくれる.
# predict関数で,式に従った先の値まで「予測」する.(計算をしているだけだが……)
predict.years.df <- data.frame("年" = seq(1977, 2050, by=1))
predict.temp <- predict(result.lm, newdata=predict.years.df) # 戻ってくるのは目的変数だけなのでベクトル扱いできる
plot(df$'年', df$'八王子.ave', type='l', xlab='year', ylab='Ave. of Aug. Temp.', xlim=c(1977,2050), ylim=c(20, 30))
par(new=TRUE)
plot(predict.years.df$'年', predict.temp, type='l', xlab='', ylab='', xlim=c(1977,2050), ylim=c(20, 30))(切片が大きくマイナス?と考えたかもしれないが,説明変数が1977からスタートしていることに注目.この切片は0の時,つまり西暦0年の時の8月の気温に相当する.実際にそんなことはないと思うので,産業革命以降に気温の上昇が始まった,つまり産業革命以降の実際の記録から回帰分析すれば,もっと傾きが大きくなる,と考えるのが妥当だろう)
傾きのところ,つまりaの内容の一番右に表示されているp値(Pr(>|t|)に注目.これはt検定などでいうところのp値である.特に回帰係数aに対応する帰無仮説と対立仮説は,それぞれ以下のようになる.
- 帰無仮説: x1つまり説明変数は,目的変数に影響を与えない.
- 対立仮説: x1説明変数は,目的変数に影響を与える変数である.
という風になる.すなわちこのp値が0.05を超えている場合は,帰無仮説が棄却されず「なんか回答が得られたけど,実際のところ,この変数は影響与えてないよねー」という意味になる.
今回は明確に傾きが影響していることがわかっているのでp値は低いが,説明変数が複数である重回帰分析ではこのp値を見ながら説明変数のセットを探していくことになる.