今回は,「気温以外のデータ」を使って,太平洋側の都市と日本海側の都市の分類器を作成してみる.
線形二項分類
線形分類(Linear Classification)とは,2つのカテゴリが入っているデータの集合の真ん中に一本直線を引くことで,カテゴリ分けする境目を定め,予測したいデータが入ってきた時に,どちらかに分類する問題である.もちろん人間が一本線を引くことで行うこともできるが,これを機械学習で行う.
入力するデータが2次元,例えば「降水量,日照時間」だった場合には,カテゴリ分けする境目は「直線」になるが,「降水量,日照時間,湿度」のように3次元になると「2次元平面」になり,「降水量,日照時間,湿度,風速」のように4次元だと「3次元超平面」になる.
3次元空間上の平面ぐらいは平面に表示するグラフでなんとか表示できるものの,4次元以上は無理なので,写像をするか「4次元の線形の式」として理解するしかない.
本項では,線形Support Vector Machine(Linear SVM)と,ロジスティック回帰(Logistic Regression)による,分類器というか,つまり直線に必要な「係数」および「切片」を学習する.
ロジスティック回帰は「回帰」と名がついているが,分類問題に使う.分ける直線を学習するので「線形回帰」とも言えるので,この名前がついている.
ダミー変数とカテゴリ変数
日本海側と太平洋側の年を分類すると書いたが,SVMやロジスティック回帰で機械学習するためには,これを数字に直さなければならない.もちろん太平洋側と日本海側は大小の比較ができないなど「値」としては,意味がないわけで,ここでは太平洋側を0,日本海側を1として表すことにする.
このように,その要素の有無で0と1の2値で表現される変数,その大小や差に意味がないものを「ダミー変数」と呼ぶ.(回帰分析でもダミー変数を使うことができる.)
例えば北海道の都市のように「太平洋側,日本海側,オホーツク海側」のように3つ以上の状態があり,2値で表すことができないもの,つまり「0, 1, 2, 3...などの状態が複数あり,かつその数字が大小の意味を持ってない場合」は,カテゴリ変数と呼ぶ
カテゴリ変数は二項分類つまりここでおこなような「AとBのどっち?」の問題では扱えないので,カテゴリ変数で表現している内容を,要素に分けて,要素の有無で表現,つまり複数のダミー変数に直すなどの方法をとる.
データの取得と加工
例によって,気象庁オープンデータのページから,
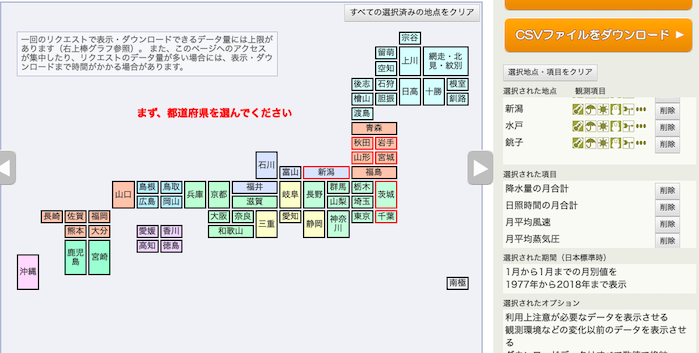
都市は,秋田県→秋田市,岩手県→宮古市,山形県→酒田市,宮城県→石巻市,新潟県→新潟市,茨城県→水戸市,千葉県→銚子市,の順で,それぞれ選択.
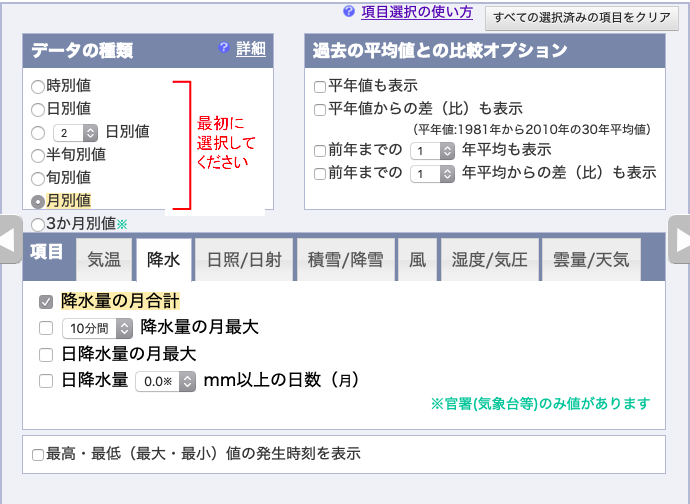
月別の値を選択し,降水量の月合計,
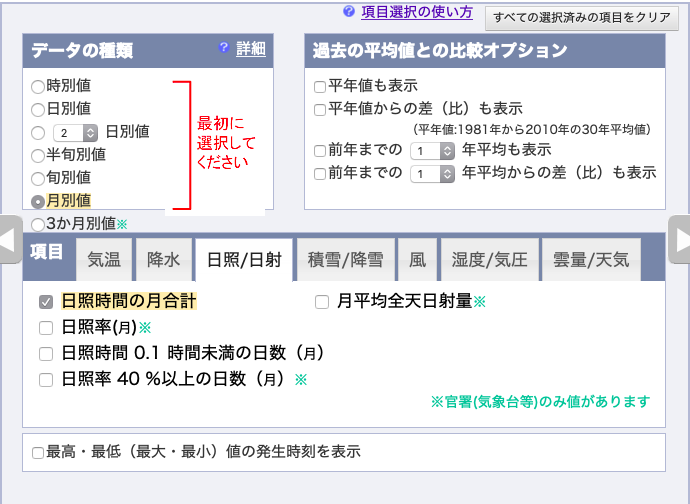
日照時間の月合計,
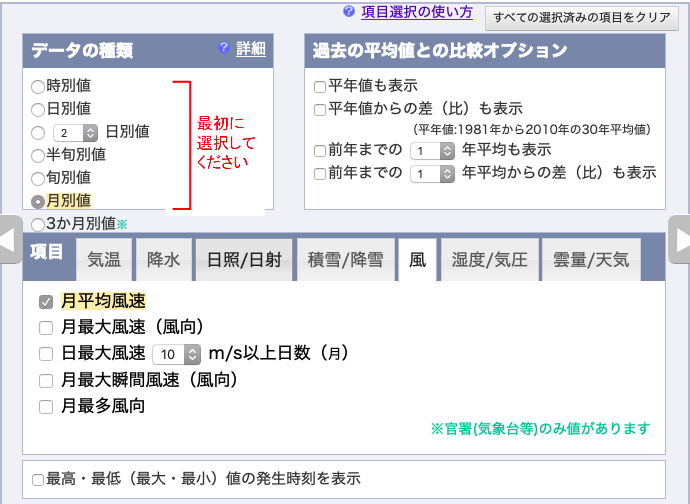
月平均風速,
湿度/気圧の月平均蒸気圧,を選択し,
1977年〜2018年の「1月」のデータをダウンロードする.
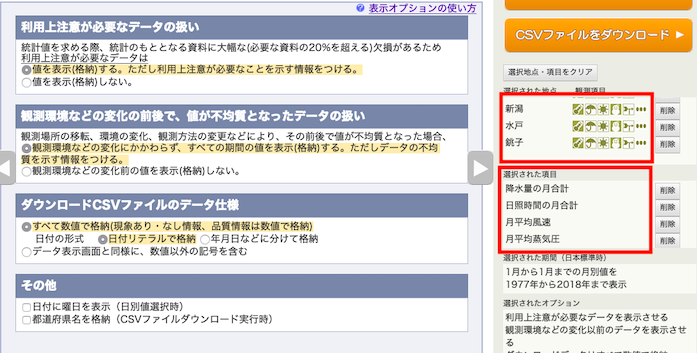
表示オプションはデフォルト.地点の順番と,項目の順番を確認すること.
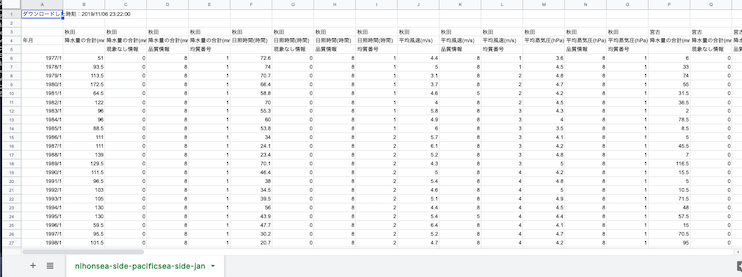
ダウンロードしたCSVはこんな見た目になる.
このCSVを「太平洋側日本海側ダミー変数」を加えたスタック形式のデータに加工する.
Google Spreadsheetに上記CSVを読み込んだ状態.
例によって不要な行と列を削除する.降水量に関しては「現象なし情報」という列も含まれているので注意.
秋田, 宮古, 酒田, 石巻, 新潟, 水戸, 銚子を抽出するために新しいスプレッドシートのワークブックを作る.
ワークブック名とシート名を整える
変数名・列名を入れる.観測地点,太平洋側日本海側ダミー,降水量の合計,日照時間,平均風速,平均蒸気圧.
太平洋側日本海側ダミー変数は,太平洋側を0,日本海側を1と決めておく.
元のワークブックから,秋田の1977年〜2018年のデータを選択して,右クリック→コピー.
新しいワークブックの方の降水量のセルを指定して,右クリック→貼り付け.列の場所を間違えないように.
貼り付けられた状態.
観測地点列の頭に「秋田」を記入し,コピー.
その下,41行(残り41年分)の行の観測地点の列を選択して,貼り付け.
太平洋側日本海側ダミーの列に「1」を記入.前述のように太平洋側の都市が0で,日本海側の都市が1,秋田は「1」.コピー.
その下,41行(残り41年分)の行の太平洋側日本海側ダミーの列を選択して,貼り付け.
貼り付けられた状態.
同じように宮古(太平洋側),
酒田(日本海側),
石巻(太平洋側),
新潟(日本海側),
水戸(太平洋側),
銚子(太平洋側)のデータを作成する.
いつもと同じように,新しい方のワークブックのシートをファイル→ウェブに公開.
シートを,CSVとして公開する
いつものようにRに読み込んで,最初の数行を表示する.
url <- '公開したURL'
df <- read.csv(url, header=TRUE)
head(df)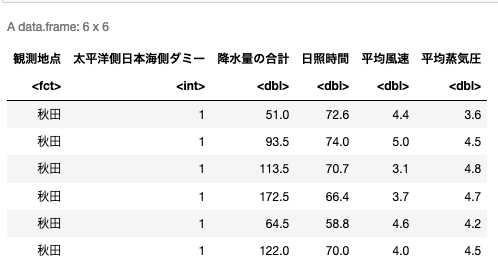
訓練データとテストデータ
前述の通り,線形二項分類は「データをうまく判別できるような直線を引く」ことで分類を行うが,これは言い換えれば,直線を表す式 y = ax + b のaとbを「機械学習」することである.
機械学習とは,自動的に「学習」の手順を定めて繰り返し行うことで,厳密ではないものの正解に近い解(近似解)に徐々に近づけていくことであるが,その時に訓練データ(トレーニングデータ)とテストデータの2つのデータセットを用いる.
訓練データを使って学習して,訓練データで表現される正解に近づいていくのは当然と言えば当然で,そこで学習の過程で「訓練データを使って学習して,テストデータでどれだけ正解に近いかを判別する」という流れを取る.そのために訓練データとテストデータは別のものにしておく必要がある.
とは言っても実際には「今持っているデータの半分を訓練データとして使い,残り半分をテストデータとして使うように指示する」だけである.スタック形式のデータが1000行分あれば,ランダムに500行抽出して訓練データとし,残り500行をテストデータにする,という形である.これはRのdata.frameの機能を使うと簡単に実現できる.
# 行数を取得する
num.of.row <- nrow(df)
# 行数からランダムに行番号を抽出.第2引数に0.5をかけているのは,半分抽出するという意味
random.indexes <- sample(num.of.row, num.of.row*0.5)
print(random.indexes)
# 定規の行番号だけを抽出
training.data <- df[random.indexes, ]
# 「それ以外の行」をテストデータとして抽出 与えるindexesの配列に-をつけてやる
test.data <- df[-random.indexes, ]
# 確認
head(training.data)
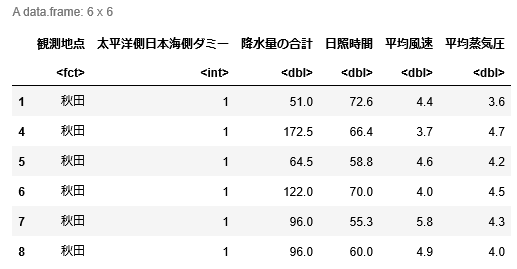
# こっちは「以外」なので順番に並んでいる
head(test.data)出力は以下のようになる.
[1] 107 97 30 185 36 214 28 225 45 227 98 166 2 57 109 129 197 31
[19] 67 190 77 13 246 79 251 104 12 212 168 167 207 240 143 159 53 58
[37] 48 213 82 39 187 9 118 144 216 3 84 252 199 194 127 130 183 74
[55] 141 90 124 112 234 27 65 161 235 42 249 37 162 181 135 89 153 20
[73] 120 145 114 232 182 95 76 186 176 193 147 75 119 202 11 32 66 158
[91] 78 247 71 248 121 128 35 210 241 189 203 17 41 63 50 138 61 101
[109] 102 110 163 223 115 140 87 123 188 175 43 69 85 220 177 179 180 221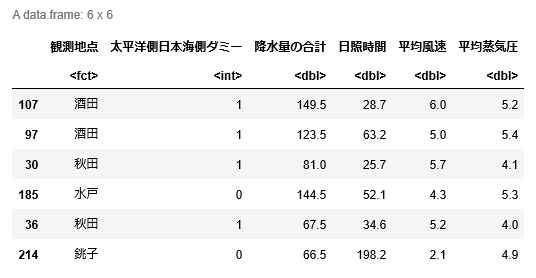
線形2項分類の目的変数と説明変数,SVM分類期の学習の実施
Rの標準パッケージの中にはSVMは含まれていないので,まずkernlabという追加パッケージをインストールする.インストールするといっても下のプログラムを実行するという形である.
# 線形2項分類を行う線形SVMのためのパッケージを入れる
install.packages("kernlab")
library(kernlab)「真ん中に直線を引くので,実はやっていることは回帰分析とは変わらない」と前述したが,「2項分類」なので,目的変数は0か1(kernlabのksvmの場合,実際にはここに文字列の値が入っていても良い),説明変数が観測データとなる.
したがって,formulaに与える式は,太平洋側日本海側ダミー ~ .となる.ただしkernlabのksvmはformula=キーワードをつけずに式を直接第1引数に入れるようになっている.(なぜRの基本から外れた実装になっているのかは不明)
今回はダミー変数が目的変数なので,type="C-svc"を入れておくと,ダミー変数を目的変数とした二項分類になる.またデータを標準化・正規化したいのでscaled=TRUEも入れておく.
その後,一度受け取った変数をそのまま1行に書いて「実行」する.
学習が終わったら,テストデータの説明変数だけを抽出したものを食わせて,太平洋側か日本海側の0か1を予測させる.
# 観測地点は不要なので落とす
training.data.df <- training.data[, c('太平洋側日本海側ダミー','降水量の合計', '日照時間', '平均風速', '平均蒸気圧')]
# 回帰のように,式formulaとdata.frameを与える.
# ただしksvmはformula=キーワードを書かずに,第1引数に直接式を書いてやる.
# 今回のようにダミー変数をyに置きたい場合には,type="C-svc"を選択する.
svm.model <- ksvm(太平洋側日本海側ダミー ~ ., data=training.data.df, type="C-svc")
# ここで変数で受け取ったものを「実行する」という行が必要
svm.model
# predict関数で学習済みのSVMにテストデータの説明変数部分を食わせて,予測を得て,test.result変数で受ける
test.result = predict(svm.model, test.data[, c('降水量の合計', '日照時間', '平均風速', '平均蒸気圧')])
# 実際の正解とtest.result変数の中に入っている予測値をtable関数で比較する
table(test.result, test.data[, '太平洋側日本海側ダミー'])結果は以下のようになる.
Support Vector Machine object of class "ksvm"
SV type: C-svc (classification)
parameter : cost C = 1
Gaussian Radial Basis kernel function.
Hyperparameter : sigma = 0.773251281075058
Number of Support Vectors : 55
Objective Function Value : -21.9573
Training error : 0.031746
test.result 0 1
0 86 10
1 2 28結果は最後の表になる.正解は0つまり太平洋側なのに1つまり日本海側と予測された観測値のセットが2つあり,また,正解は1つまり日本海側なのに0つまり太平洋側と予測された観測値のセットが10個ある,ということになる.現状では正解率はあまりよくないようだ.
ksvm関数にオプションで指定する学習パラメータをうまく調整してやると,この学習率が上がることもある.また前項で触れた「標準化・正規化」のような前処理を予めデータに対してかけておくなどの方法も考えられる.
では,さらに未知のデータを食わせてみよう.
# 鳥取県境(日本海側),静岡県石廊崎(太平洋側)の2018年1月のデータを入れてみて,ちゃんと分類できるか検証する.
# 境のデータ 降水量191.5(mm), 日照時間58.1(時間), 平均風速2.6(m), 平均蒸気圧6.3(hPa),
# 石廊崎のデータ 降水量 93.5(mm), 日照時間188.6(時間), 平均風速6.8(m), 平均蒸気圧6.6(hPa)
sakai.X <- data.frame('降水量の合計'=c(191.5), '日照時間'=c(58.1), '平均風速'=c(2.6), '平均蒸気圧'=c(6.3))
print(predict(svm.model, sakai.X))
irouzaki.X <- data.frame('降水量の合計'=c(93.5), '日照時間'=c(188.6), '平均風速'=c(6.8), '平均蒸気圧'=c(6.6))
print(predict(svm.model, irouzaki.X))先ほどの学習効率がよくない状態のSVMにこのデータを食わせたら,両方とも0と出力された.つまり日本海側の堺も太平洋側と判断されてしまったことになる.
最初のテストデータの結果を見る限り,この4つの観測値,つまり降水量の合計,日照時間,平均風速,平均蒸気圧を使って太平洋側か日本海側を判別すると,太平洋側の都市を日本海側だと間違うことはあまりなく,日本海側の都市を太平洋側と間違うことが多いようだ.
つまり,1月の降水量,1月の日照時間,1月の風速平均,1月の湿度の4つの観測値は,日本海側と太平洋側を判定するのには不十分である,と言える.別の観測値を使って予測精度を上げてみよう.