主成分分析
これまで「8月の平均気温」「8月の日最高気温の月平均」「8月の日最低気温の月平均」「25度を超えた日数」という4つの観測値を扱ってきた.この「4つの観測値から『都市の気候』をうまく表現したい.うまく説明できるようにしたい.」という問題を考える.
ところが,観測値が4つある時,つまり説明変数が4つある時,2次元グラフはそれぞれの軸の組み合わせて6通り存在する.さらに3つ以上の観測値を軸にして見ることはできないため,グラフでぱっと見ではわからない.
そこで「主成分分析」という「次元削減」手法を用いる.
主成分分析は,説明変数が多数存在する時に,元のデータの特徴を十分に表しつつ,かつ次元が少ない説明変数のセットを「合成」する手法である.
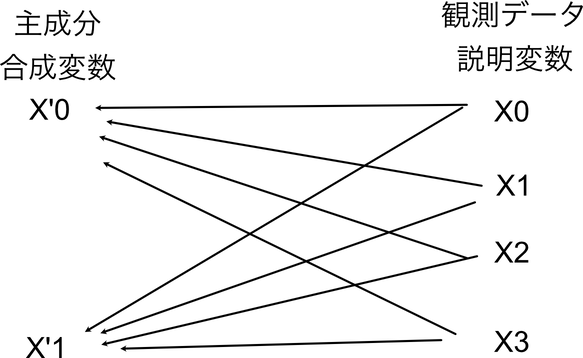
実際のには,上図のようにただ足し合わせるだけではなく,変換行列を作成し,それによって次元削減をするが,その変換行列を作成する際に「元のデータの特徴を十分に表現できる」ことを目標として調整をしていく.
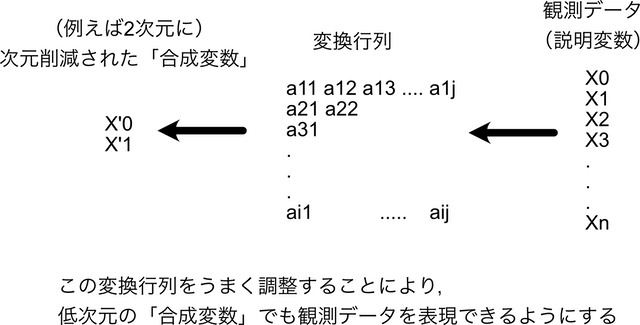
これは3DCGのレンダリングの時の3次元座標から2次元座標の変換行列(カメラの位置,アングル,拡大度等から算出される)を「3Dモデルのディティールが上手く掴める」ように調整するのに,イメージ的には近い.

十分に表現できるような「カメラの位置」「カメラの角度」「画角」「拡大」などをうまく調整し,3Dデータの特徴を十分に表現できるような2次元画像にするのと,主成分分析のための変換行列の作成は,似たようなもんである.
使用するデータと加工
今回はデータとして,相関係数を出した時と同じ「東日本の県庁所在地」の「1977年〜2018年」の「8月の平均気温」「8月の日最高気温の月平均」「8月の日最低気温の月平均」「25度を超えた日数」のCSVファイルを使う.
さらにそこから,盛岡,甲府,横浜に絞ってスタック形式のデータを作る.
GoogleスプレッドシートにCSVを読み込む.
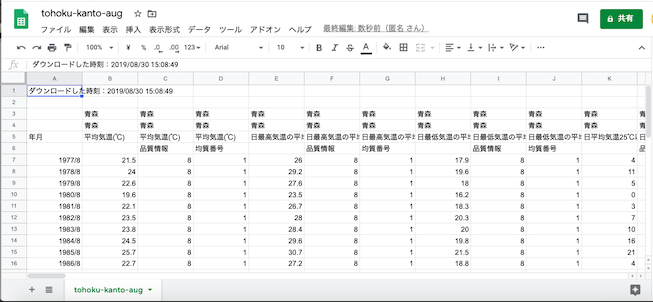
例によって不要な行と列を削除.
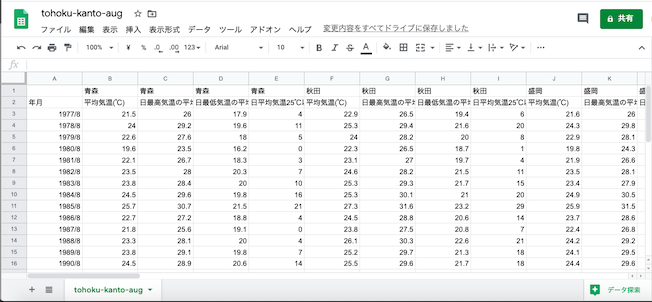
左下の「+」マークを押して,新規シートを追加.
シートの名前をわかりやすくつける.
最初のシートから盛岡の全データをコピーして,
新作ったシートに貼り付ける.(一番左の列は地点ラベルが入るので,2番目の列から貼り付ける)
盛岡のデータが貼り付けられた状態.
一番左の列名を「観測地点」にして,
1つのセルに「盛岡」と書き込んでコピーし,
データの他の行に貼り付ける
盛岡のデータは完成.
同じように甲府のデータもコピペして地点ラベルをつける.
横浜のデータも同様にする.
列名を,Rでも読み込める短いものにする.
新しく作ったスタック形式のシートを右クリックし「別のワークブックにコピー」→「新しいスプレッドシート」(Rは公開されたURLの関係上,単一ブックに単一シートでないと読み込めないようだ)
コピーされた新しいスプレッドシートを開く
新しいスプレッドシートの名前を整えて,
いつものようにCSVでウェブに公開してURLを取得しておく.
url <- '公開したURL'
df <- read.csv(url)
head(df)いつものようにRで読み込み,冒頭数行を表示.
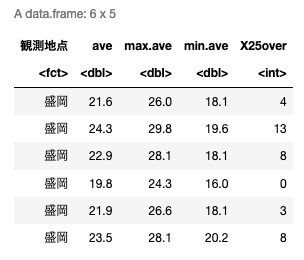
生のデータの散布図を描く
まず,説明変数4つをx軸とy軸に取り,2次元のグラフを描画している.説明変数の組み合わせは合計6通りあるが,とりあえず3つの組み合わせでグラフを描画する.
# スタック形式のデータを行指定でバラしてから,
library(stats)
morioka.df <- df[c(1:42), ]
kofu.df <- df[c(43:84), ]
yokohama.df <- df[c(85:126), ]
# X軸を平均気温,Y軸を日最高気温の月平均の散布図でプロットする
plot(morioka.df$ave, morioka.df$max.ave, col=2, xlim=c(18, 30), ylim=c(22, 36), ann=FALSE)
par(new=TRUE)
plot(kofu.df$ave, kofu.df$max.ave, col=3, xlim=c(18, 30), ylim=c(22, 36), ann=FALSE)
par(new=TRUE)
plot(yokohama.df$ave, kofu.df$max.ave, col=4, xlim=c(18, 30), ylim=c(22, 36), xlab='Ave. temp. of Aug.', ylab='Ave. of max temp. of aug.')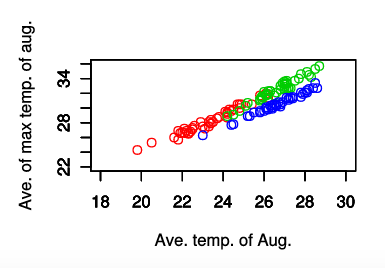
X軸が「8月の平均気温」,Y軸が「8月の日最高気温の平均」
# X軸を日最高気温の月平均, Y軸を日最低気温の月平均の散布図でプロットする
plot(morioka.df$max.ave, morioka.df$min.ave, col=2, xlim=c(24, 36), ylim=c(16, 26), ann=FALSE)
par(new=TRUE)
plot(kofu.df$max.ave, kofu.df$min.ave, col=3, xlim=c(24, 36), ylim=c(16, 26), ann=FALSE)
par(new=TRUE)
plot(yokohama.df$max.ave, kofu.df$min.ave, col=4, xlim=c(24, 36), ylim=c(16, 26), xlab='Ave of max temp. in Aug.', ylab='Ave. of Min temp. of Aug.')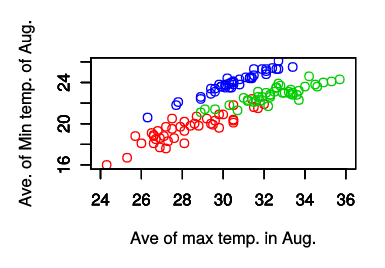
X軸が「8月の日最高気温の平均」,Y軸が「8月の日最低気温の平均」
# X軸を日最低気温の月平均, Y軸を25度を超えた日数の散布図でプロットする
plot(morioka.df$min.ave, morioka.df$X25over, col=2, xlim=c(16, 26), ylim=c(0, 31), ann=FALSE)
par(new=TRUE)
plot(kofu.df$min.ave, kofu.df$X25over, col=3, xlim=c(16, 26), ylim=c(0, 31), ann=FALSE)
par(new=TRUE)
plot(yokohama.df$min.ave, kofu.df$X25over, col=4, xlim=c(16, 26), ylim=c(0, 31), xlab='Ave of min temp. in Aug.', ylab='Count of over 25 degree in Aug.')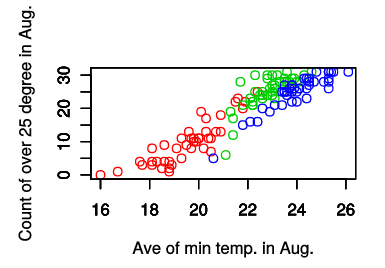
X軸を日最低気温の月平均, Y軸を25度を超えた日数
今は都市ごとに色分けをしているため判別しやすいが,青(col=4)で示された横浜はどのグラフでも分離して見える(線形判別分析が簡単にできそう,すなわち判別の「直線」を引くことが可能に見える,「線形分離可能」と呼ぶ.)のに対して,盛岡と甲府はかなり被っているように見える.(盛岡と甲府は同じ直線上に載っているように見える)
主成分分析は「このグラフが分離して見えるような表示になるような「合成変数」を作成すること」が目的である.合成変数は任意の数(次元)で作成することができる.合成変数を2つ(2次元)にしてしまえば,2次元グラフでも簡単に表示できるようになるはず.
主成分分析の実行
prcomp関数を使う.
各変数の単位が異なっている(ここでは摂氏の温度と,日数の2つの単位が混在している)場合には,「正規化」or「標準化」を行う必要がある.prcomp関数の場合にはscale=TRUEオプションを入れれば良い.
# 各変数の単位(ここでは摂氏何度とか,日数の2つの単位が混在している)が異なっている時は,「正規化」or「標準化」を行わなければならない.
# prcomp関数の場合は,scaleオプションをTRUEにする
# まず目的変数と説明変数に分ける
city.name = df[, 1] # 1列目の全ての行をcity.nameに
city.param = df[, 2:5] # 2列目から5列目までの全ての行をcity.paramに
# 説明変数を正規化をして主成分析にかける
pca.results <- prcomp(city.param, scale=TRUE)
summary(pca.results)
# princomp という関数もあるが,これはサンプルサイズと変数の数に制限があるもの結果表示は以下の通り.
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.9295 0.47388 0.22170 0.05831
Proportion of Variance 0.9307 0.05614 0.01229 0.00085
Cumulative Proportion 0.9307 0.98686 0.99915 1.00000PCというのは主成分, 合成変数の英語であるPrincipal Componentの略語である.元の変数の数と同じだけ計算されるが,寄与率Proportion of Variance,および累積寄与率Cumulative Proportionに注目する.
寄与率というのは,それぞれの主成分つまり合成変数が「データをどれだけ表現できているか」を表したものである.寄与率の合計(累積寄与率)が1.0に十分に近ければ,合成変数のみでデータを十分表現できていると言っても良い.
今回は2番目の主成分までで累積寄与率が0.987に達しており,計が1に十分に近いので,この2次元だけで元データを十分に表現していると言って良い.つまり「4次元あった変数は2次元に落とし込むことが可能」ということである.
逆に合計寄与率が低かった場合,「この次元数では元のデータを表現できているとは言い難い」となる.この場合,合成変数して用いる次元数を増やす必要がある.1次元ずつ増やしていって,寄与率が1に十分近くなる次元数を探す.次元数を増やしても合計寄与率が上がらなくなった場合はそこで止める.
今回は第3主成分の寄与率が0.012であり,第2主成分までで累積寄与率が0.986つまり98.6%説明できることから,第2主成分までを用いる.(端的にいえば2次元の散布図1枚で描画できるようにするためである)
変換行列の取得と変換,第2主成分までを使った散布図の描画
predict関数に,主成分分析の結果と,新しいデータ(今回は古いデータをそのまま使っている)を食わせることで,主成分を計算することができる.
先にレンダリングに例えて変換行列と書いたが,predict関数はその「特徴をうまくとらえたレンダリング」を行うのと同じである.
レンダリングの結果を第2主成分(2番目の合成変数)までを使って(つまり2次元のみを使って),再び散布図に描画する.つまり「X軸が第1主成分,Y軸が第2主成分」である.
# 結果を使って主成分を計算し
PCs <- predict(pca.results, newdata=city.param)
# 第2主成分までを2次元に散布図で描く
morioka.pcs <- PCs[c(1:42), ]
kofu.pcs <- PCs[c(43:84), ]
yokohama.pcs <- PCs[c(85:126), ]
plot(morioka.pcs[, 1], morioka.pcs[, 2], col=2, xlim=c(-4.0, 3.0), ylim=c(-1.0, 1.0), ann=FALSE)
par(new=TRUE)
plot(kofu.pcs[, 1], kofu.pcs[, 2], col=3, xlim=c(-4.0, 3.0), ylim=c(-1.0, 1.0), ann=FALSE)
par(new=TRUE)
plot(yokohama.pcs[, 1], yokohama.pcs[, 2], col=4, xlim=c(-4.0, 3.0), ylim=c(-1.0, 1.0), xlab='PC1', ylab='PC2')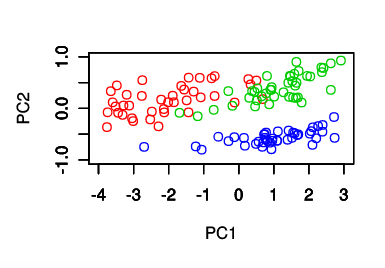
合成変数の散布図では,盛岡,甲府,横浜が綺麗に分離しており,線形判別分析が容易になっている.この3都市の8月の気温に関しては,主成分分析 - 合成変数が有効であることを示している.
この状態で最初の目的である「4つの観測値から『都市の気候』をうまく表現したい.うまく説明できるようにしたい.」を達成できたかを考えると,「直線の補助線を引くことで,「この線のこちら側が盛岡で,この線のこちら側が甲府で,この線のこちら側が横浜です」とうように明確に説明できるようになる」ので,目的を達成したと言える.