[Work/Class/Rの基礎とデータ処理/r_stat]

CSVデータからのt検定

回帰分析の項と同じく，気象庁のオープンデータを使う．

今回は，1977年〜2018年の，江戸川臨海，東京，青梅，八王子，練馬，府中の5箇所の，1月の月平均気温データと，8月の月平均気温データをCSVとしてダウンロードしておく．

これをやるためには2つのファイルに分けるのが一番楽っぽいので，同時点で期間の月のところを変えて，2つCSVファイルをダウンロードする．

ダウンロードした状態は，それぞれ以下から参照すること．

t検定とは

今回は，東京湾の海風が吹き付ける江戸川区と，内陸の練馬区で，月平均気温が違うかどうかをみる．

小中学校までなら，単純に「1977年から2018年までの平均を出してそれを比較すれば良い」と考えるかもしれないが，回帰分析の項で見た様に，平均気温は年単位で周期的な動きを見せるなど，安定しておらず，単に平均をとって比較するだけでは「それが本当に正しいのか」には大きく疑問が出てしまう．

「2つの気温データ群の間の差を，統計的に（ある程度）保証してくれる」のがt検定である．

「絶対的な保証」ではないが，「ある程度は」保証してくれる，と考えると良い．

2つ群間の検定には，

  1. 2群間に対応がある場合(2つの変数の間に何らかの従属関係がある場合)
  2. 2群間に対応ない場合の2つ(2つの変数は全く独立)

の2つがある．

1.の「2群間に対応がある場合」は，例えば「食事の前の血糖値と食事後の血糖値との比較」を考えてみると良い．この場合，データとしては「Aさんの食事前と食事後」「Bさんの食事前と食事後」「Cさんの食事前と食事後」……という対になるデータが必要である．

気温で考えてみると「同じ年の（1月の）平均気温で，江戸川と練馬に差があるか」になる．

この場合，月平均気温データが年ごとにペア対応している必要がある．

ペアのデータはこんな感じ「1977年の練馬の1月の気温, 1977年の江戸川の1月の気温」,「1978年の練馬の1月の気温, 1978年の江戸川の1月の気温」,「1979年の練馬の1月の気温, 1979年の江戸川の1月の気温」……このように年ごとに違う地点が並んでいれば良い．（順番はちゃんと並んでいなくても良い）

帰無仮説と対立仮説，p値

この様な統計処理の場合，「否定したい」帰無仮説と，帰無仮説が否定されることで（ある程度）保証される対立仮説の2つで，仮説を定義する．

「観測地点により，年ごとに考えても平均気温に差がある」ことを示したい場合，帰無仮説が「地点での平均気温差がない」であり，その帰無仮説が否定されると（ある程度保証される）のが「観測地点での平均気温の差がある」である．

この「ある程度保証する」の「ある程度」を表すのが，検定の結果出てくるp値という値である．p値が0.05「以下」の時，「5%水準で，有意差がある」（つまり「差がある」）なんて言い方をする．一般的に5%が統計的に「差がある」という水準．これが10%になると「値は色々違うけれど，統計的に立ちかめてみると，実は大した差がない」ぐらいの感覚で捉えておくと良い．

内部計算的には信頼区間とかが出くるが，詳しい説明は統計の教科書を読むこと．

データの整え方

Googleスプレッドシートに，まず1月のCSVを読み込む

1月のCSV

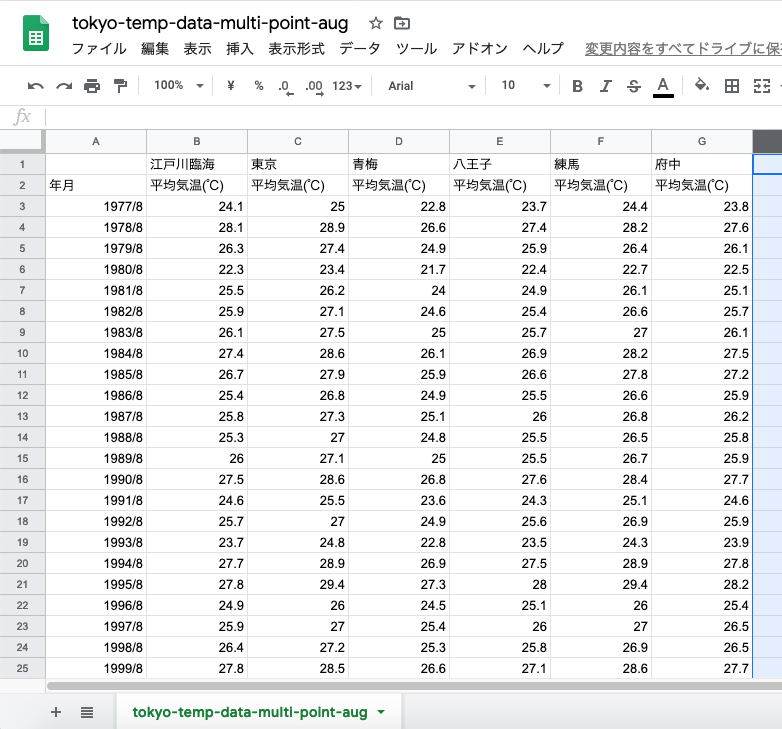
前回と同じように，不要な行と列を削除する．

不要な行と列の削除

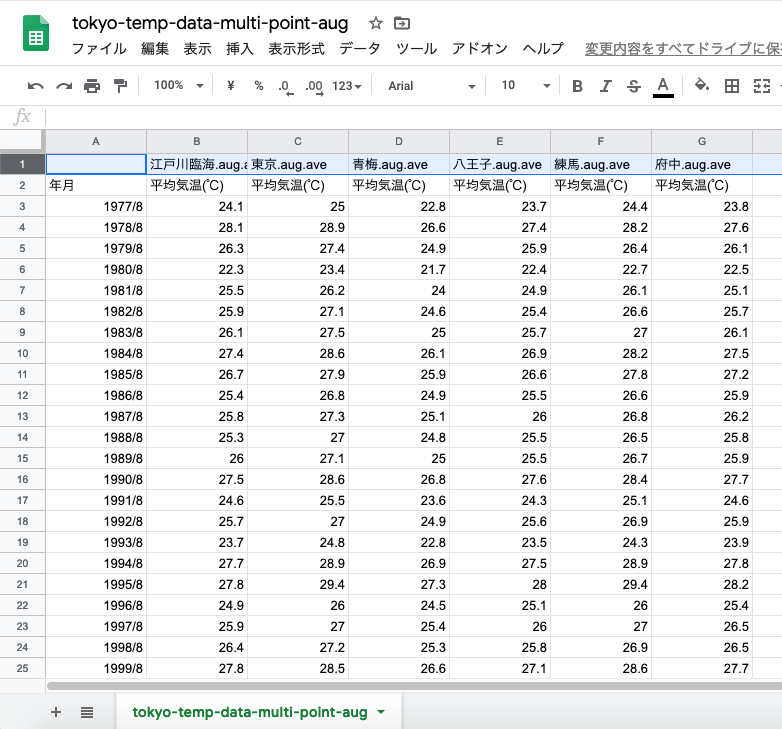
列名を整える．前回やったように，長い列名だとRの標準のdata.frame形式では読み込めない．短く「地点.jan.ave」にしておく．

列名を整える

「平均気温」の行も削除．

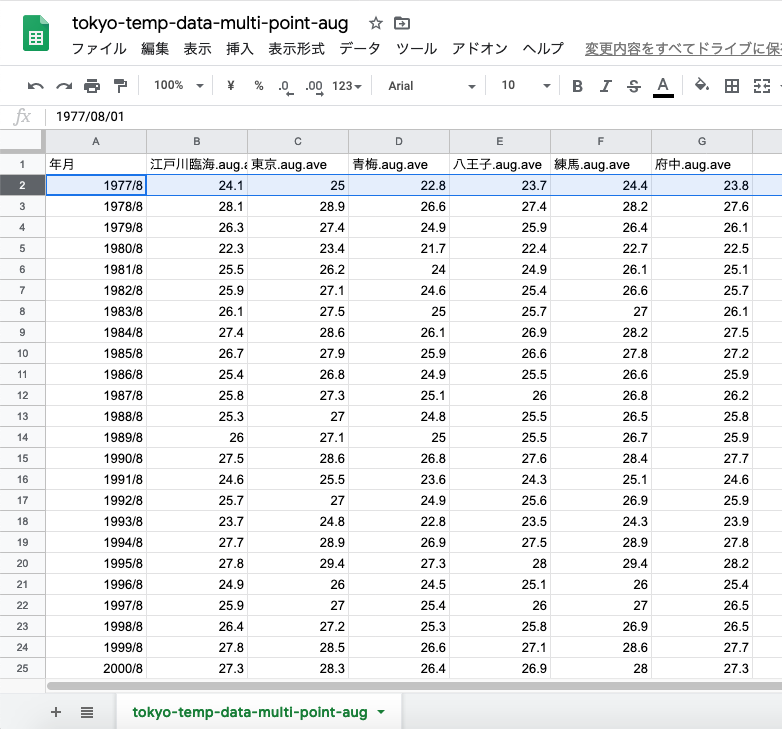
元の列名の行も削除

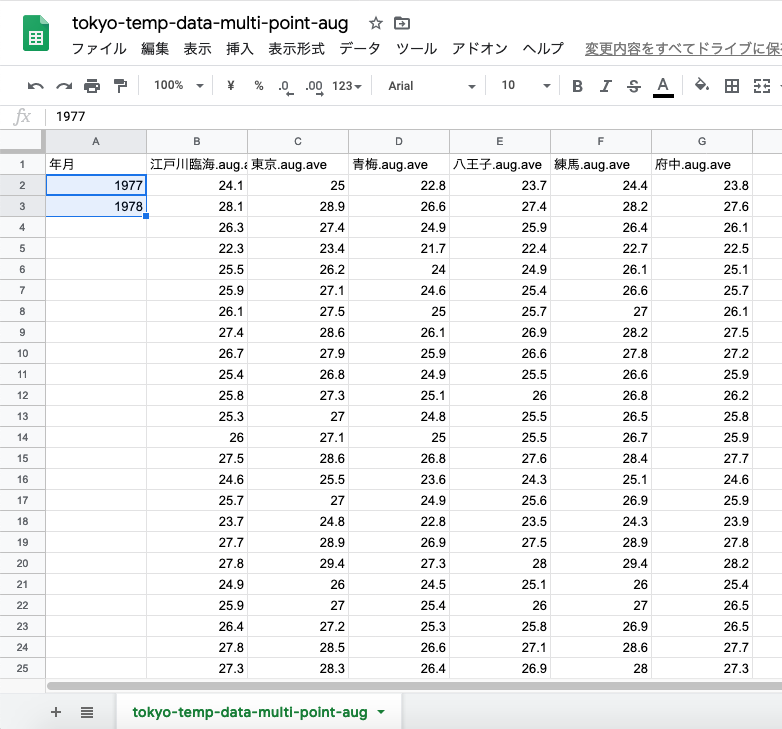
年月の列を「1977/1」から「1977」の形へ整える．「1977」年と「1978」年のセルの中身を変えて，

最初の2年分だけ値を入れて

2年分を選択し，右下の四角を下に引っ張る．

右下の四角を下に引っ張る

それ以降の年が補完される．

年が補完される

同様に8月のCSVも別に読み込み，処理していく．

（処理すべきCSVシートが2枚以上で，同じ操作で整える場合，本来ならこの部分整える部分もプログラムで書いて自動化する．しかしRの標準のdata.frameではそれができない．data.frameを拡張したいくつかのクラスがあるので，それを使うと可能になる．Pythonは実質的に標準になっているpandas.DataFrameというライブラリで，同じ処理を複数のシートに対して行うことが得意なので，データが大量にある時はPythonの方が書きやすい．）

8月のCSV 不要な行と列の削除 列名を整える 元の列名の行も削除 最初の2年分だけ値を入れて 右下の四角を下に引っ張る 年が補完される

8月のシートのデータの部分だけを選択し，右クリックから「コピー」

8月のシートのデータ部分だけを選択

1月のシートの右端を選択し，右クリックから「貼り付け」して，2つのシートをくっつける．

1月のシートへ8月のデータをくっつける

くっついた状態．列名が正しいことを確認する．（同じ列名だと読み込めない）

1月と8月のデータがくっついた状態

スプレッドシートのファイル名を「1月と8月両方入ってますよ」と変更し，

スプレッドシートのファイル名を変更

シートの名前も同じように変更する．

シートの名前を同じように変更

前々回，前回と同じように「ファイル」→「ウェブに公開」

ファイル→ウェブに公開

公開するシートを選択し，カンマ区切り形式（CSV）を選択して公開し，URLをコピーしておく．

公開するシートの選択と，カンマ区切り形式を選択．

前々回，前回と同じように，以下のコードで読み込んで，最初の数行を表示する． 

url <- 'Googleスプレッドシートで公開したURL'
df <- read.csv(url, header=TRUE)  #　header=TRUE　は第１行が列の変数名
head(df)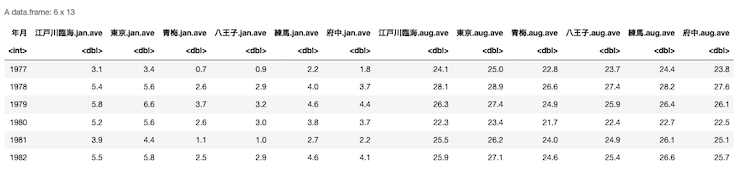
1月と8月をまとめてRに読み込んで最初の数行を表示した状態．

欠損値

こうやって作成したdata.frameを最初の数行だけではなくprint(df)して，後ろの方までよく眺めると，2009年8月の江戸川臨海のデータが「NA」となっており，「欠損」していることを発見できる．「2群間に関係性のないt検定」では問題は起きないが，「2群間に関係性のあるt検定では，2地点を比較した時に片方にだけ値がないと，エラーを起こす．

そこで「行を丸ごと」削除するという方法を取る．今回は1977年〜2018年と比較的長い期間なので，1年分ぐらいデータがなくても，まぁ大勢は変わらないだろう，という判断である．これが10年分のデータがないとなると，大きく影響が出るので，その場合は他の対策を考える．

Rのデータフレームで，欠損値のある行を丸ごと削除するのは以下のコードで行う． 

# 欠損値のある行を削除して，df変数に再代入
df <- na.omit(df)

今度はNAと表示されているところがないか，再度printして確認する．

平均を求める

まず，江戸川と練馬の1月と8月の気温の平均を求める．

これまでやってきたように，data.frameの変数名$列名で，その列をベクトルとして取り出せる．そのベクトルをmean()関数に入れると，そのベクトルの平均を求められる．下の例ではその結果をそのままprint関数に入れている． 

print(mean(df$'江戸川臨海.jan.ave'))
print(mean(df$'練馬.jan.ave'))
print(mean(df$'江戸川臨海.aug.ave'))
print(mean(df$'練馬.aug.ave'))

出力は以下のようになる． 

[1] 5.597561
[1] 4.453659
[1] 26.36098
[1] 27.11707

1977年〜2018年の間の月平均気温は，1月は江戸川の方が暖かく，8月は練馬の方が暑い，ということになる．平均では明確に差があるが，これが「偶然」なのか，それとも「何らかの原因があって明確に異なっている」のかを，統計的に明らかにする（事実ではない）のがt検定である．

分散が等しいかどうかのF検定

t検定を行うためには，比較したい2つの群の「分散」がある程度等しいことが求められる．F検定というものを使う．

F検定の帰無仮説は「2群の分散は等質である」，対立仮説は「2群の分散は等質であるとは言えない」である． 

var.test(df$'江戸川臨海.jan.ave', df$'練馬.jan.ave')

を実行すると，以下の結果が得られる． 

	F test to compare two variances

data:  df$江戸川臨海.jan.ave and df$練馬.jan.ave
F = 0.97042, num df = 40, denom df = 40, p-value = 0.9248
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.5175003 1.8197201
sample estimates:
ratio of variances 
         0.9704152

この時，p-valueと表示されている値が0.92であり，0.05以下でないことから，5%水準で「2群の分散が等質である」という帰無仮説は棄却されないので，t検定（Studentのt検定）を使うことができる．

（ちなみにF検定の帰無仮説が棄却されてしまった時は「Welchのt検定」という方法を使う）

2群間に関係性のあるt検定

まず「2群間に関係性のあるt検定」を行う．

同じ月の江戸川と練馬の平均気温のペアが必要であるが，並びが揃っている2つ1次元配列，すなわち2つの配列の同じ場所に比較したい同じ年の平均気温が入っている形で与えてやる．

それを検定にかける．

  1. 帰無仮説は「二つの集団の間に差がない」 = 「同じ年の江戸川と練馬の1月（8月）の月平均気温の間には，差がない」
  2. 対立仮説は「二つの集団の間に差がある」 = 「同じ年の江戸川と練馬の1月（8月）の月平均気温の間には，差がある」

であり， 結果のp値が0.05を下回っていれば，「差がある」と見るべきである．

この場合，

  1. 同じ年で違う地点でのデータが，二つの地点の配列の並びの中で，同じ場所にある
  2. 「何年」なのかは順不同になる．つまり古い順とか新しい順に並んでいる必要はない

という2つのベクトルの形にして食べさせれば良い．つまりF検定と同じようになる．1月の江戸川と練馬の気温の「2群間に関係があるt検定」を実行するには，以下のコードを使う． 

t.test(df$'江戸川臨海.jan.ave', df$'練馬.jan.ave', paired=TRUE)

このt検定のコードのpaired=TRUEという部分が，「2群間に関係性のあるt検定」を指定している．前述したように「ペア」の値を見るためpairedというオプションである．

結果は以下の通り． 

	Paired t-test

data:  df$江戸川臨海.jan.ave and df$練馬.jan.ave
t = 27.581, df = 40, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 1.060080 1.227725
sample estimates:
mean of the differences 
               1.143902

p-value，つまりp値の値が，2.2e-16，つまり「2.2かける10の-16乗」である．これは0.05よりも充分に小さいことから，帰無仮説「同じ年の江戸川と練馬の1月の月平均気温の間には，差がない」が5%水準で棄却され，「差がある」という対立仮説が採用されたことになる．

同じように8月の江戸川と練馬の月平均気温の「2群間に関係があるt検定」をしてみる． 

t.test(df$'江戸川臨海.aug.ave', df$'練馬.aug.ave', paired=TRUE)

結果は以下のようになる． 

	Paired t-test

data:  df$江戸川臨海.aug.ave and df$練馬.aug.ave
t = -11.707, df = 40, p-value = 1.699e-14
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.8866303 -0.6255648
sample estimates:
mean of the differences 
             -0.7560976

p値が，1.699e-14，つまり「1.699かける10の-14乗」なので，0.05よりも充分に小さいことから，帰無仮説「同じ年の江戸川と練馬の8月の月平均気温の間には，差がない」が5%水準で棄却され，「差がある」という対立仮説が採用されたことになる．

2群間に対応がない場合のt検定とコード例

2群間に対応がない場合は，本当にただの値の集合2つの差を見る時に行われる．

先ほどは「年ごと」に対応させて検定したが，対応がない場合「（1977年〜2018年まで「全ての年をひっくるめて」）東京湾の海風が吹き付ける湾岸の江戸川は，風が吹き抜けない練馬に比べ）8月の平均気温が低い」という仮説を検証することになる．

（実際にt検定を行うときは，この「対応がない場合」がほとんどである）

先に出した平均気温を見た時に，確かに江戸川の方が練馬よりも8月の平均気温は低いが，それを統計的に保証するための検定をする．

この場合の，帰無仮説は「（1977年から2018年にかけての）江戸川と練馬の8月の月平均気温の間には，差がない」であり，対立仮説は「（1977年から2018年にかけての）江戸川と練馬の8月の月平均気温には差がある」である． 

t.test(df$'江戸川臨海.jan.ave', df$'練馬.jan.ave', var.equal=TRUE)
t.test(df$'江戸川臨海.aug.ave', df$'練馬.aug.ave', var.equal=TRUE)

var.equal=TRUEオプションは，先ほどのF検定の結果の「分散が同じかどうか」である．FALSEにすると自動的にWelchのt検定になる．結果は以下の通り． 

	Two Sample t-test

data:  df$江戸川臨海.jan.ave and df$練馬.jan.ave
t = 4.6782, df = 80, p-value = 1.16e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.6573019 1.6305030
sample estimates:
mean of x mean of y 
 5.597561  4.453659 
 
 	Two Sample t-test

data:  df$江戸川臨海.aug.ave and df$練馬.aug.ave
t = -2.4771, df = 80, p-value = 0.01535
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.3635334 -0.1486617
sample estimates:
mean of x mean of y 
 26.36098  27.11707

8月のt検定のp値は0.015であり，0.05を十分に下回っているので，「差がない」帰無仮説は否定される，すなわち「（1977年〜2018年にかけての）8月の月平均気温は，江戸川の方が練馬よりも有意に低い」と言うことができる．

ただし，風が通っているからかどうかはこのデータからは当然わからない． 今回取得した他の「風が通る場所」と「風が通らない場所」を比較していくと，その可能性を検証できるかもしれない．試してみること．