相関係数
JISでは,相関のことを「2つの確率変数の分布法則の関係.多くの場合線形関係の程度を指す」と定義している.
要するに,比例関係にありそうな2つの軸による「2つの値のペア」が大量にあり,それをざっとみた時,どのぐらい比例関係(もしくは反比例関係)の直線上に載っているか,を示す値が「相関係数」である.
相関係数は-1から1の間を取り,1の時観測データは比例の一直線上に並ぶ.-1のときは反比例の一直線上に並ぶ.(ちなみに,相関係数0とは,傾きが全くない一直線上に並ぶことを示すが,ほとんどの場合相関係数は算出できない)
実世界の観測データには常にノイズが載っていて一直線上に並ぶことはありえないので,相関係数が1や-1というのはありえないのだが,1や-1に近いほど「線形モデルに理想的に近い」ということができる.

上図が,観測値の数(サンプル数)が多い時の,相関係数に従った分布のイメージである.
相関係数が高いほど比例の直線に綺麗に載るようになり,逆に低いほどバラつきがある.自然現象は「正規分布」という分布に従うことが多いが,サンプル数が多いとこのようにグラフ上で綺麗に見ることができる.逆にサンプル数が少ない時はグラフに表示してもぱっと見ではわからない.そこで「観測された値は正規分布に従う」前提で相関係数を出して,サンプル数が少ない時でも全体のばらつきを「相関係数」として知ることができるようになる.
相関係数が-1.0から0までの負の値の時は,反比例の直線が基準になる.
本項では,「緯度(北緯)が大きければ大きいほど,つまり北の観測地点ほど,8月の気温が低くなる,緯度と8月の気温に負の相関がある,と仮定し,その相関係数を確かめる.
気象庁オープンデータ
「気象庁|過去の気象データ・ダウンロード」ページから,必要なデータを絞ってCSV形式でダウンロードすることができる.これを分析対象にする.
官公庁らしく,文字コードがSHIFT-JISなので注意する.
東日本の県庁所在地の「1977年〜2018年の,8月の平均気温,8月の日最高気温の平均,8月の日最低気温の平均,8月で日平均気温が25℃を上回った日数」のデータを落としてくる.手順は以下の通り.
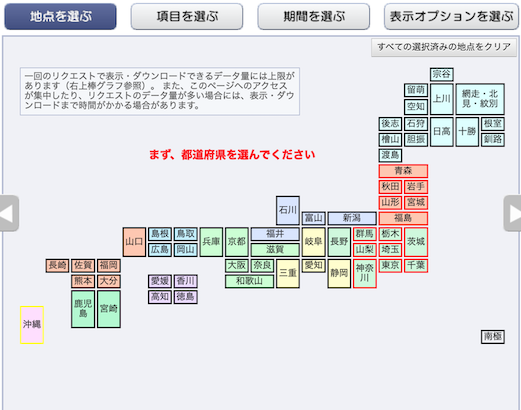
まず観測地点を選ぶ.東日本の各県をクリックし,その中で県庁所在地を選択しておく.
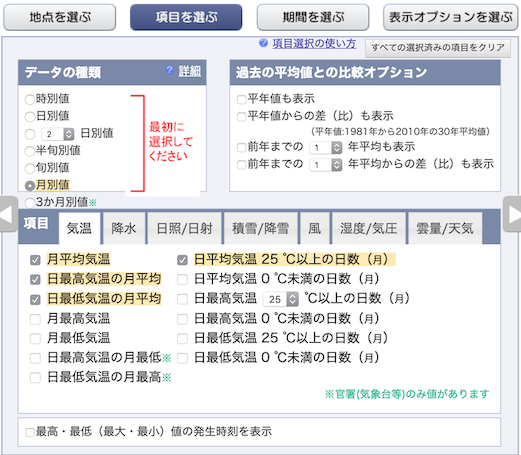
次にデータの種類を選ぶ.「データの種類」は「月別値」,「項目」は「気温」「日最高気温の月平均」「日最低気温の月平均」「日平均気温が25℃を超えた日数」を選択する.
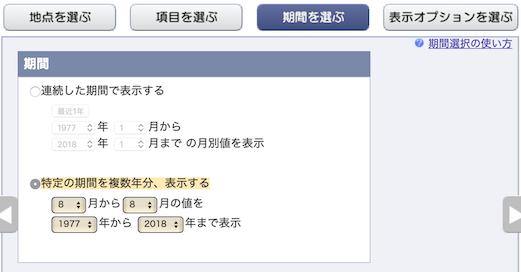
「期間」は,「8月から8月」「1977年〜2018年」つまり,各年の8月のデータだけを持ってくる.
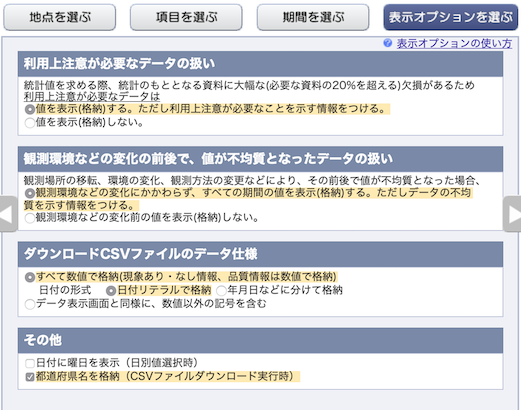
表示オプションは「都道府県名を格納」にチェックを入れておく.
この状態で,右の「CSVをダウンロード」する.
ちなみにダウンロードしたデータはこのようになる.
Google SpreadsheetでCSVを編集する
Rは標準状態では,CSV読み込み機能が実にプアで,ほとんどのオープンデータに対応できない.気象庁オープンデータも,やはりそのまま読み込むことができない.そこでCSVデータを一度表計算ソフトに読み込んで,整形する.Google Spreadsheetはブラウザから使える表計算ソフトで,さらにそのままWeb公開もできてAzure Notebookから読み込めるので,Azure Notebookを使っているときは便利.
まずGoogle Spreadsheetを開いたら,「ファイル」→「インポート」
「アップロード」タブを選択.
ファイルを投げる.
読み込みオプションはそのままで問題ない.
読み込まれた状態.
「ダウンロードした」時刻の行,「その次の行」を削除.次いで「品質情報」と「均質番号」の列を削除していく.
余分な列と行を削除した状態.
「列名」に当たる部分を作っていく.列名は1行,かつ列名の文字数制限があるので,青森の平均気温で2行を使っている部分を「青森.ave」のように1行にまとめる.
日の最高気温の月平均は「青森.max.ave」,日の最低気温の月平均は「青森.min.ave」,25度以上を記録した日数は「青森.25over」という感じに短くする.
すると以下のようになる.
Azure Notebookからすぐにアクセスできるように,WebにCSV形式で公開する.
「ファイル」→「ウェブに公開」

シートを選択し,CSV形式を選択して,「公開」
「公開」すると,URLが選択された状態で出てくるので,コピーする.
Azure NotebookのRのNotebookで,まずhttpsに対応したファイルを読み込むパッケージを入れる.
install.packages("bitops")
library("RCurl")
あとは,これまでと同じように,read.csv関数で読み込む.
url <- 'コピーしたURL'
df <- read.csv(url, header=TRUE)
head(df)data.frame形式で読み込まれた状態.ちゃんと列などが整っている.
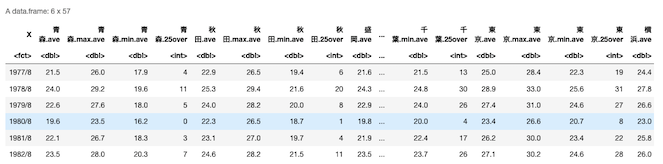
相関係数の算出
ここから,このdata.frameから必要なデータを抽出して,緯度との相関係数を算出する.
まず,1列目を落とす.すべての年を集めて順不同で用いるため.
列番号に-をつけたベクトルを与えると,その列が落ちたdata.frameが出てくるので,変数で受け取っておく.
# 今回は年月は関係ないので,年月の列を落とす
# 列番号に-をつけることで,落とすことができる.
# ただし非破壊的なので,変数で受ける必要がある
df <- df[,c(-1)]
head(df)年月の列が落ちた状態.

今回のデータは42年分のデータがある.
まず,青森の平均気温の列を取り出す.
# 42年分のデータがある
# 青森の8月の平均気温を取り出す
aomori.ave <- df[, '青森.ave'] # 青森列を取り出す.
# この場合df[行指定, 列指定]なので,行指定が空だと「この列の全ての行」の意味になる
# もちろん前にやったように,aomori.ave <- df$'青森.ave'でも可能
# Rのdata.frameは抽出してもdata.frameのままで抽出し下以外のデータも残り続けることに注意.
print(aomori.ave)printの出力結果は以下の通り.
[1] 21.5 24.0 22.6 19.6 22.1 23.5 23.8 24.5 25.7 22.7 21.8 23.3 23.8 24.5 21.5
[16] 22.5 20.6 25.9 23.6 22.2 22.7 22.0 25.8 24.8 21.4 21.9 21.3 23.1 24.9 24.4
[31] 24.6 21.9 21.9 26.0 24.2 25.3 24.7 23.6 23.6 24.5 22.0 22.8同様に日最高気温の平均を得たい場合には,
# 同様に日最高気温の平均を得たい場合には,
aomori.max <- df[, '青森.max.ave'] # 青森.max.aveとという列名がついている列を取り出す
print(aomori.max)printの出力は以下のようになる.
[1] 26.0 29.2 27.6 23.5 26.7 28.0 28.4 29.6 30.7 27.2 25.6 28.1 29.1 28.9 25.7
[16] 26.3 25.2 30.4 27.4 26.7 27.2 25.6 30.6 29.3 25.8 25.6 25.2 27.7 29.1 29.0
[31] 29.6 25.8 26.0 30.6 28.4 29.6 29.3 27.8 27.9 28.7 26.3 27.4各年に対応する緯度のベクトルを作る.今取り出したデータはすべて青森市のものなので,青森市の緯度が42個(42年分のデータに対応する数)並んだ配列を作れば良い.
# 対応する緯度のベクトルを作成する
# 青森市は北緯40.49度
aomori.longi <- rep(40.49, 42)
# 40.49を42年分繰り返したベクトルを作る
print(aomori.longi)
#当たり前だが,何月だろうと何年だろうと,緯度は変わらないので,同じ数字が続く配列で正解printの出力結果は以下の通り.
[1] 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
[13] 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
[25] 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49 40.49
[37] 40.49 40.49 40.49 40.49 40.49 40.49とりあえず,青森市の8月の平均気温について,x軸を緯度,y軸を8月の平均気温にして,散布図を描いてみる.
# とりあえず散布図を描いてみる
# x軸が緯度で,y軸は8月平均気温にする.
plot(aomori.longi, aomori.ave, col=2, xlab='longitude', ylab='average temp. of aug.')
legend("topright", c("Aomori"), ncol=1, col=2)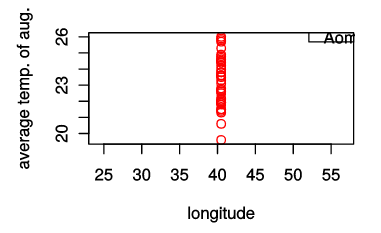
x軸が緯度で,どの年でも緯度は変わらないので,垂直に並ぶことになる.
青森が大丈夫そうなので,他の地点も全部緯度配列を作り,散布図を描いてみる.
# 同様に盛岡,仙台,福島,水戸,千葉,東京の太平洋側の県庁所在地各地についても行い,散布図として追加描画する
# 描画されるグラフが違うので,まず青森を再描画する
# xlimは緯度なので,34〜42というところだろうか.
# ylimは8月の平均気温なので,15〜35あたりだろうか
# ann=FALSEを指定することで,軸メモリやラベルは出力しない
plot(aomori.longi, aomori.ave, col=2, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 盛岡市は北緯39.42
morioka.ave = df[, '盛岡.ave']
morioka.longi = rep(39.42, 42)
par(new=TRUE)
plot(morioka.longi, morioka.ave, col=3, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 仙台市は北緯38.16
sendai.ave = df[, '仙台.ave']
sendai.longi = rep(38.16, 42)
par(new=TRUE)
plot(sendai.longi, sendai.ave, col=4, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 福島市は北緯37.45
fukushima.ave = df[, '福島.ave']
fukushima.longi = rep(37.45, 42)
par(new=TRUE)
plot(fukushima.longi, fukushima.ave, col=5, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 水戸市は北緯36.22
mito.ave = df[, '水戸.ave']
mito.longi = rep(36.22, 42)
par(new=TRUE)
plot(mito.longi, mito.ave, col=6, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 千代田区役所は北緯35.41
tokyo.ave = df[, '東京.ave']
tokyo.longi = rep(35.41, 42)
par(new=TRUE)
plot(tokyo.longi, tokyo.ave, col=7, xlim=c(34, 42), ylim=c(15, 35), ann=FALSE)
# 千葉市は北緯35.36
chiba.ave = df[, '千葉.ave']
chiba.longi = rep(35.36, 42)
par(new=TRUE)
plot(chiba.longi, chiba.ave, col=8, xlim=c(34, 42), ylim=c(15, 35), xlab='longitude', ylab='average temp. of aug.')
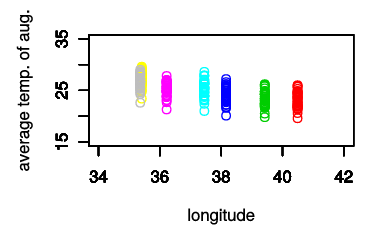
青森と同じように,観測地点ごとに1直線に並ぶ.
既に「なんとなく気温は緯度に反比例しているんじゃないかなぁ」はわかるが,幅が大きい.
緯度と8月の平均気温の相関係数を計算する.
緯度と気温のペアになるように,緯度と気温の配列をそれぞれ全て連結する.散布図を書いていることからわかるように,相関係数を計算するときはペアになっていればペア間の並びは順不同で良い.
「ピアソンの相関係数」が,一般的な相関係数である.何もオプションをつけずcorr.test関数を呼び出すと,このピアソンの相関係数になる.
明らかに間違っている値が入っている,つまり外れ値が存在する場合には「スピアマンの相関係数(順位相関係数)というのを使う.corr.test関数にmethod="spearman"オプションを与えると,スピアマンの相関係数を出せる.
# 平均気温と井戸を対応させて(同じインデックスにして),一つのベクトルに連結する
all.points.ave = c(aomori.ave, morioka.ave, sendai.ave, fukushima.ave, mito.ave, tokyo.ave, chiba.ave)
all.points.longi = c(aomori.longi, morioka.longi, sendai.longi, fukushima.longi, mito.longi, tokyo.longi, chiba.longi)
# ピアソンの相関係数を出す
cor.test(all.points.ave, all.points.longi)
# 外れ値があっても対応できるスピアマンの相関係数(順位相関係数)を出す
cor.test(all.points.ave, all.points.longi, method="spearman", exact=FALSE)
# 外れ値とは,他の値から大きく外れた値のこと.
# これが入っていると統計の計算はうまく働かないことがある
# (上記のピアソンの相関係数は外れ値の影響を受ける)
# exact=FALSEは順位相関係数の算出において,同順位がある場合ワーニングを吐くのを抑制するオプション出力結果は以下の通り.
Pearson's product-moment correlation
data: all.points.ave and all.points.longi
t = -15.711, df = 292, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.7343584 -0.6096300
sample estimates:
cor
-0.6768226
Spearman's rank correlation rho
data: all.points.ave and all.points.longi
S = 7178900, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.6950137 相関係数が-0.677.相関係数は1〜0〜-1の値をとるので,-0.677は結構高めの負の相関があることになる.
負の相関は反比例を表す.緯度が大きくなればなるほど,8月の平均気温が低くなるので,間違ってはいない.
相関係数は,あくまで相関の度合いなので,相関係数だけで全ての説明できるわけではないが,同じく8月の日最高気温,日最低気温,日平均気温25℃以上の日数についても,緯度に対する相関係数を算出して比較することには意味がある.ので他の気温についても相関係数が高いものを見つける.
このデータだとスピアマンの相関係数は,若干相関係数が高いと出るようだ.つまり観測データには外れ値が存在すると言うことになる.例えば極端な冷夏などがあったのであろうか.
p-valueというのは「p値」と呼ばれるもので,この値が(一般的に)0.05をきっている場合には,「相関があることを程度統計的に言うことができる」という意味である.詳しくは検定の項目で後述する.今は両方とも2.2e-16つまり「2 * 10の-16乗」なので,十分に0.05を下回っているので,相関がある,と言うことができる.
8月の平均気温と緯度の相関係数が出たので,8月の日最高気温の月平均,8月の日最低気温の月平均,8月の25度を超えた日数,についても,それぞれ緯度との相関係数を出してみる.
# 平均気温と緯度の相関係数が出たので,
# 他の列,日の最高気温の月平均,日の最低気温の月平均,25度を超えた日数の相関係数と緯度の相関係数も出してみる
aomori.max.ave <- df[, '青森.max.ave']
aomori.min.ave <- df[, '青森.min.ave']
aomori.25over <- df[, '青森.25over']
morioka.max.ave <- df[, '盛岡.max.ave']
morioka.min.ave <- df[, '盛岡.min.ave']
morioka.25over <- df[, '盛岡.25over']
sendai.max.ave <- df[, '仙台.max.ave']
sendai.min.ave <- df[, '仙台.min.ave']
sendai.25over <- df[, '仙台.25over']
fukushima.max.ave <- df[, '福島.max.ave']
fukushima.min.ave <- df[, '福島.min.ave']
fukushima.25over <- df[, '福島.25over']
mito.max.ave <- df[, '水戸.max.ave']
mito.min.ave <- df[, '水戸.min.ave']
mito.25over <- df[, '水戸.25over']
tokyo.max.ave <- df[, '東京.max.ave']
tokyo.min.ave <- df[, '東京.min.ave']
tokyo.25over <- df[, '東京.25over']
chiba.max.ave <- df[, '千葉.max.ave']
chiba.min.ave <- df[, '千葉.min.ave']
chiba.25over <- df[, '千葉.25over']
# 連結する
all.points.max.ave <- c(aomori.max.ave, morioka.max.ave, sendai.max.ave, fukushima.max.ave, mito.max.ave, tokyo.max.ave, chiba.max.ave)
all.points.min.ave <- c(aomori.min.ave, morioka.min.ave, sendai.min.ave, fukushima.min.ave, mito.min.ave, tokyo.min.ave, chiba.min.ave)
all.points.25over <- c(aomori.25over, morioka.25over, sendai.25over, fukushima.25over, mito.25over, tokyo.25over, chiba.25over)# まず日の最高気温の月平均と井戸のピアソンの相関係数を出す
cor.test(all.points.max.ave, all.points.longi)
# 次に日の最低気温の月平均と緯度のピアソンの相関係数を出す
cor.test(all.points.min.ave, all.points.longi)
# 最後に25度を超えた日数と緯度のピアソンの相関係数を出す
cor.test(all.points.25over, all.points.longi)結果は以下の通り.
Pearson's product-moment correlation
data: all.points.max.ave and all.points.longi
t = -10.421, df = 292, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.5993465 -0.4319865
sample estimates:
cor
-0.5206503
Pearson's product-moment correlation
data: all.points.min.ave and all.points.longi
t = -19.954, df = 292, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8040740 -0.7065408
sample estimates:
cor
-0.7595445
Pearson's product-moment correlation
data: all.points.25over and all.points.longi
t = -15.982, df = 292, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.7396680 -0.6168818
sample estimates:
cor
-0.6830721 結果を見ると,緯度との相関が一番強いのは「日最低気温の月平均」であることがわかった.つまり「最高気温と緯度との関係よりも,気温が下がりづらいことと緯度の関係が強い」ということである.
ただし相関係数はあくまで相関であり,因果関係ではない.因果を統計的に説明する必要があるので,次の線形回帰分析,重回帰分析を行う必要がある.